Question

【题目】如图，在△ABC中，AB=AC，BC=4，面积是16，AC的垂直平分线EF分别交AC，AB边于点E、F，若点D为BC边上的中点，点M为线段EF一动点，则△CDM周长的最小值为（ ）

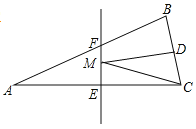
A.4B.8C.10D.12

Answer 1

【答案】C

【解析】

连接AD，AM，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再再根据EF是线段AC的垂直平分线可知，点C关于直线EF的对称点为点A，故AD的长为CM＋MD的最小值，由此即可得出结论．

解：连接AD，AM．

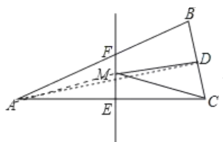
∵△ABC是等腰三角形，点D是BC边的中点，
∴AD⊥BC，
∴，

解得：AD＝8，
∵EF是线段AC的垂直平分线，
∴点C关于直线EF的对称点为点A，
∴MA＝MC，
∵AD≤AM＋MD，
∴AD的长为CM＋MD的最小值，
∴△CDM的周长最短＝（CM＋MD）＋CD＝AD＋BC＝8＋×4＝8＋2＝10．
故选：C．