题目内容
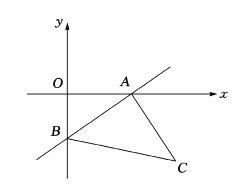
【题目】如图,在平面直角坐标系中,已知一次函数![]() 的图像与x轴交于点
的图像与x轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)在坐标系中能否找到点![]() ,使得
,使得![]() 且
且![]() ?如果能,求出满足条件的点
?如果能,求出满足条件的点![]() 的坐标;如果不能,请说明理由.
的坐标;如果不能,请说明理由.
【答案】(1)![]() ;(2)(3,3)或(1,-1)
;(2)(3,3)或(1,-1)
【解析】
(1)由待定系数法将点A,B的坐标代入即可求得;
(2)根据点P在线段AB的垂直平分线上,且点P到AB中点的距离等于AB的一半进行求解,构造全等三角形得到点P的坐标.
解:(1)∵直线AB经过点A(4,0),B(0,2)
代入y=kx+b中,得![]() ,
,
解得: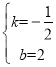 ,
,
∴AB的解析式为:![]() ;
;
(2)如图,点P在AB的垂直平分线上,且∠APB=90°,
可知△APB为等腰直角三角形,
过点P作y轴的垂线于点M,过A作MP的垂线于点N,
∵AB=![]() =
=![]() ,
,
∴BP=AP=![]() =
=![]() ,
,
∵∠MPB+∠APN=90°,∠APN+∠PAN=90°,
∴∠BPM=∠PAN,
在△PBM和△APN中,
 ,
,
∴△PBM≌△APN(AAS)
∴MB=PN,MP=AN,
设MB=x,则AN=MP=x+2,
∴在直角△MBP中,
MB2+MP2=BP2,
即![]() ,
,
解得:x=1,
∴MP=AN=3,
点P的坐标为(3,3),

同理:如图,当点P在直线AB下方时,
有△BMP≌△PNA(AAS),
设MP为y,则OM=AN=y,BM=4-y,
在直角△BMP中,
BM2+MP2=BP2,
即(2+y)2+y2=![]() ,
,
解得:y=1,
∴MP=1=OM,
即点P坐标为(1,-1)
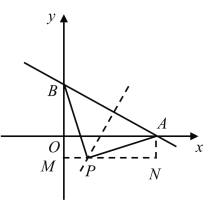
综上:能够找到点P满足条件,点P坐标为(3,3)或(1,-1).

练习册系列答案
相关题目