题目内容
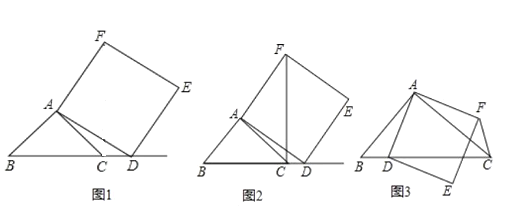
【题目】如图①,在△ABC中,![]() 为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如图②,如果AB=AC,![]() ,当点D在线段BC的延长线上时,猜想线段CF、BD的关系,并说明理由.
,当点D在线段BC的延长线上时,猜想线段CF、BD的关系,并说明理由.
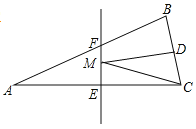
(2)如图③,如果AB![]() AC,
AC,![]() 是锐角,点D在线段BC上,当
是锐角,点D在线段BC上,当![]() 时,必有CF
时,必有CF![]() BC(点C,F不重合),请先在横线上添加条件,再作证明.
BC(点C,F不重合),请先在横线上添加条件,再作证明.
【答案】(1)CF=BD且CF⊥BD,理由见解析;(2)45,证明见解析.
【解析】
(1)CF与BD关系为互相垂直且相等.首先证明△DAB≌△FAC,然后得出CF=BD,∠ACF=45°,∠BCF=∠ACB+∠ACF=90°,即可求得答案;
(2)当∠ACB=45°时,过点A作AG⊥AC交CB或CB的延长线于点G,则∠GAC=90°,可推出∠ACB=∠AGC,所以AC=AG,于是得到CF⊥BD.
解:(1)结论:CF=BD且CF⊥BD,
理由:∵∠FAD=∠BAC=90°
∴∠BAD=∠CAF,
∵![]() ,
,
∴![]() ,
,
在△BAD与△CAF中,
∵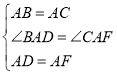 ,
,
∴△BAD≌△CAF(SAS),
∴CF=BD,∠ACF=∠ACB=45°,
∴∠BCF=90°
∴CF⊥BD.
故答案为:CF=BD且CF⊥BD;
(2)当∠ACB=45°时,必有CF⊥BC.
理由:过点A作AC的垂线与CB所在直线交于G ,
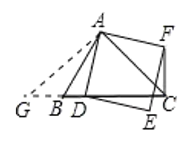
则∵∠ACB=45°,
∴AG=AC,∠AGC=∠ACG=45°,
∵AG=AC,AD=AF,
∵∠GAD=∠GAC∠DAC=90°∠DAC,∠FAC=∠FAD∠DAC=90°∠DAC,
∴∠GAD=∠FAC,
∴△GAD≌△CAF(SAS),
∴∠ACF=∠AGD=45°
∴∠GCF=∠ACG+∠ACF=90°
∴CF⊥BC

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目