题目内容
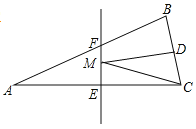
【题目】如图,⊙O是△ABC的外接圆,∠ABC=45°,AD是⊙O的切线交BC的延长线于D,AB交OC于E.
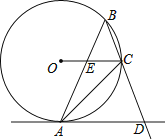
(1)求证:AD∥OC;
(2)若AE=2![]() ,CE=2.求⊙O的半径和线段BE的长.
,CE=2.求⊙O的半径和线段BE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连结OA,根据切线的性质得到OA⊥AD,再根据圆周角定理得到∠AOC=2∠ABC=90°,然后根据平行线的判定即可得到结论;
(2)设⊙O的半径为R,则OA=R,OE=R-2,AE=2![]() ,在Rt△OAE中根据勾股定理可计算出R=4;作OH⊥AB于H,根据垂径定理得AH=BH,再利用面积法计算出OH=
,在Rt△OAE中根据勾股定理可计算出R=4;作OH⊥AB于H,根据垂径定理得AH=BH,再利用面积法计算出OH=![]() ,然后根据勾股定理计算出AH=
,然后根据勾股定理计算出AH=![]() ,则HE=AE-AH=2
,则HE=AE-AH=2![]() -
-![]() =
=![]() ,再利用BE=BH-HE进行计算.
,再利用BE=BH-HE进行计算.
试题解析:(1)连结OA,如图,
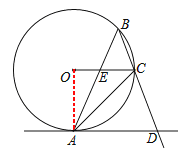
∵AD是⊙O的切线,
∴OA⊥AD,
∵∠AOC=2∠ABC=2×45°=90°,
∴OA⊥OC,
∴AD∥OC;
(2)设⊙O的半径为R,则OA=R,OE=R-2,AE=2![]() ,
,
在Rt△OAE中,∵AO2+OE2=AE2,
∴R2+(R-2)2=(2![]() )2,解得R=4,
)2,解得R=4,
作OH⊥AB于H,如图,OE=OC-CE=4-2=2,
则AH=BH,
∵![]() OHAE=
OHAE=![]() OEOA,
OEOA,
∴OH=![]() =
=![]() ,
,
在Rt△AOH中,AH=![]() ,
,
∴HE=AE-AH=2![]() -
-![]() =
=![]()
∴BH=![]() ,
,
∴BE=BH-HE=![]() -
-![]() =
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目