题目内容
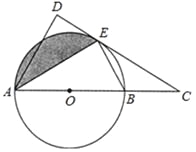
【题目】(8分)如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.
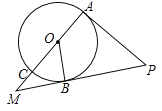
(1)求证:PB是⊙O的切线;
(2)当OB=3,PA=6时,求MB,MC的长.
【答案】(1)证明见试题解析;(2)MB=4,MC=2.
【解析】
试题(1)由切线的性质,得到∠MAP=90°,由直角三角形的性质,得到∠P+M=90°,由余角的性质,得到∠M+∠MOB=90°,可得∠MOB=90°,根据切线的判定,可得答案;
(2)根据△OBM∽△APM,可得![]() ,根据解方程组,可得答案.
,根据解方程组,可得答案.
试题解析:(1)∵PA切⊙O于点A,∴∠MAP=90°,∴∠P+M=90°.∵∠COB=∠APB,∴∠M+∠MOB=90°,∴∠MOB=90°,即OB⊥PB,∵PB经过直径的外端点,∴PB是⊙O的切线;
(2)∵∠COB=∠APB,∠OBM=∠PAM,∴△OBM∽△APM,∴![]() ,∴
,∴![]() ①,
①,![]() ②,解得MB=4,MC=2,∴当OB=3,PA=6时,MB=4,MC=2.
②,解得MB=4,MC=2,∴当OB=3,PA=6时,MB=4,MC=2.

练习册系列答案
相关题目