题目内容
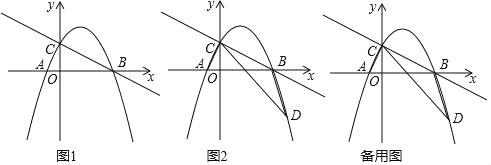
【题目】如图,在矩形ABCD中,AB=6,BC=4,点E是边BC上一动点,把△DCE沿DE折叠得△DFE,射线DF交直线CB于点P,当△AFD为等腰三角形时,DP的长为_____.
【答案】![]() 或
或![]()
【解析】
先根据AD=BC=4,DF=CD=AB=6,得出AD<DF,再分两种情况进行讨论:①当FA=FD时,过F作GH⊥AD与G,交BC于H,根据△DGF∽△PHF,得出![]() ,求得PF的长,进而得出DP的长;②当AF=AD=4时,过F作FH⊥BC于H,交DA的延长线于G,根据勾股定理求得FG,FH的长,再根据△DFG∽△PFH,得出
,求得PF的长,进而得出DP的长;②当AF=AD=4时,过F作FH⊥BC于H,交DA的延长线于G,根据勾股定理求得FG,FH的长,再根据△DFG∽△PFH,得出![]() ,求出PF的长,即可得出PD的长.
,求出PF的长,即可得出PD的长.
∵AD=BC=4,DF=CD=AB=6,∴AD<DF,故分两种情况:
①如图1所示,当FA=FD时,过F作GH⊥AD于G,交BC于H,则HG⊥BC,DG![]() AD=2,∴Rt△DFG中,GF
AD=2,∴Rt△DFG中,GF![]() ,∴FH=6﹣4
,∴FH=6﹣4![]() .
.
∵DG∥PH,
∴△DGF∽△PHF,
∴![]() ,即
,即![]() ,
,
解得:PF![]() 6,
6,
∴DP=DF+PF=6![]() ;
;
②如图2所示,当AF=AD=4时,过F作FH⊥BC于H,交DA的延长线于G,则
Rt△AFG中,AG2+FG2=AF2,即AG2+FG2=16;
Rt△DFG中,DG2+FG2=DF2,即(AG+4)2+FG2=36;
联立两式,解得:FG![]() ,
,
∴FH=6![]() .
.
∵∠G=∠FHP=90°,∠DFG=∠PFH,
∴△DFG∽△PFH,∴![]() ,即
,即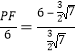 ,
,
解得:PF![]() 6,∴DP=DF+PF=6
6,∴DP=DF+PF=6![]() .
.
故答案为:![]() 或
或![]() .
.

【题目】在课堂上,老师将除颜色外都相同的1个黑球和若干个白球放入一个不透明的口袋并搅匀,让全班同学依次进行摸球试验,每次随机摸出一个球,记下颜色再放回搅匀,下表是试验得到的一组数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 |
摸到黑球的次数m | 26 | 37 | 49 | 124 | 200 |
摸到黑球的频率 |
|
|
|
| a |
![]() 表中a的值等于______;
表中a的值等于______;
![]() 估算口袋中白球的个数;
估算口袋中白球的个数;
![]() 用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
用画树状图或列表的方法计算连续两名同学都摸出白球的概率.