题目内容
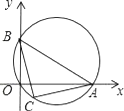
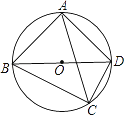
【题目】已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )
A. AC=BC+CD B. ![]() AC=BC+CD C.
AC=BC+CD C. ![]() AC=BC+CD D. 2AC=BC+CD
AC=BC+CD D. 2AC=BC+CD
【答案】B
【解析】
在CD延长线上截取DE=BC,连接EA,证明△ABC≌△ADE,进而得到△CAE是等腰直角三角形,即可得出结论.
在CD的延长线上截取DE=BC,连接EA,
∵∠ABD=∠ACB=∠ABD=45°,
∴AB=AD,
∵∠ADE+∠ADC=180°,
∠ABC+∠ADC=180°,
∴∠ABC=∠ADE,
在△ABC与△ADE中,
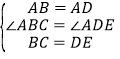 ,
,
∴△ABC≌△ADE(SAS),
∴∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE=90°,
∴∠ACD=∠ABD=45°,
∴△CAE是等腰直角三角形,
∴AC=AE,AC2+AE2=CE2,
∴ ![]() AC=CE,
AC=CE,
∴ ![]() AC=CD+DE=CD+BC,
AC=CD+DE=CD+BC,
故选B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】在课堂上,老师将除颜色外都相同的1个黑球和若干个白球放入一个不透明的口袋并搅匀,让全班同学依次进行摸球试验,每次随机摸出一个球,记下颜色再放回搅匀,下表是试验得到的一组数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 |
摸到黑球的次数m | 26 | 37 | 49 | 124 | 200 |
摸到黑球的频率 |
|
|
|
| a |
![]() 表中a的值等于______;
表中a的值等于______;
![]() 估算口袋中白球的个数;
估算口袋中白球的个数;
![]() 用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
用画树状图或列表的方法计算连续两名同学都摸出白球的概率.