题目内容
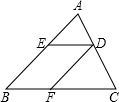
如图,△ABC中,AB=AC,AD交BC边于点M,BD=
AC,∠BAC=∠ABD=120°,则BM:MC的值是______;作△ABC的中线CF交AM于G,则CG:GF的值是______.

| 1 |
| 2 |

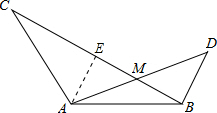
过点A作AE⊥BC于E.
∵AB=AC,∠BAC=120°,
∴BE=CE,∠C=∠ABC=30°.
设BD=k,则AB=AC=2k.
在△BDM中,∠DBM=∠ABD-∠ABM=120°-30°=90°.
在△ABE中,∵∠AEB=90°,∠ABE=30°,AB=2k,
∴AE=k.
在△AME与△DMB中,
∵
,
∴△AME≌△DMB(AAS),
∴EM=BM,
∵CE=BE=BM+EM=2BM,
∴MC=EM+CE=3BM,
∴BM:MC=BM:3BM=
;
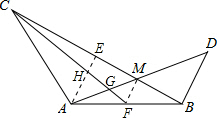 如图,作△ABC的中线CF交AM于G,设CF与AE交于点H,连接FM.
如图,作△ABC的中线CF交AM于G,设CF与AE交于点H,连接FM.
∵EM=BM,AF=BF,
∴FM∥BD,FM=
BD=
k.
∵AE∥BD,
∴FM∥AE,
∴
=
=2,
=
=
,
∴CH=2HF,HE=
FM=
×
k=
k,
∴AH=AE-HE=k-
k=
k.
∵
=
=
=
,
令HG=4t,则GF=3t,HF=7t,CH=14t,
∴CG=CH+HG=18t,
∴CG:GF=18t:3t=6.
故答案为
;6.
∵AB=AC,∠BAC=120°,
∴BE=CE,∠C=∠ABC=30°.
设BD=k,则AB=AC=2k.
在△BDM中,∠DBM=∠ABD-∠ABM=120°-30°=90°.
在△ABE中,∵∠AEB=90°,∠ABE=30°,AB=2k,
∴AE=k.
在△AME与△DMB中,
∵
|
∴△AME≌△DMB(AAS),
∴EM=BM,
∵CE=BE=BM+EM=2BM,
∴MC=EM+CE=3BM,
∴BM:MC=BM:3BM=
| 1 |
| 3 |
 如图,作△ABC的中线CF交AM于G,设CF与AE交于点H,连接FM.
如图,作△ABC的中线CF交AM于G,设CF与AE交于点H,连接FM.∵EM=BM,AF=BF,
∴FM∥BD,FM=
| 1 |
| 2 |
| 1 |
| 2 |
∵AE∥BD,
∴FM∥AE,
∴
| CH |
| HF |
| CE |
| EM |
| HE |
| FM |
| CE |
| CM |
| 2 |
| 3 |
∴CH=2HF,HE=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
∴AH=AE-HE=k-
| 1 |
| 3 |
| 2 |
| 3 |
∵
| HG |
| GF |
| AH |
| FM |
| ||
|
| 4 |
| 3 |
令HG=4t,则GF=3t,HF=7t,CH=14t,
∴CG=CH+HG=18t,
∴CG:GF=18t:3t=6.
故答案为
| 1 |
| 3 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目