Question

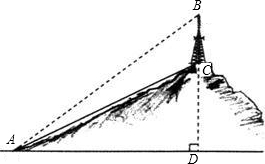
如图所示，一块四边形土地，其中∠ABD=120°，AB⊥AC，BD⊥CD，AB=30

3

m，CD=50

3

m，则这块土地的面积为______m²．

Answer 1

如图，延长CA，DB交于点P，
∵∠ABD=120°，∠ACD=60°，
在Rt△CDP中，tan∠ACD=

PD

CD

，
∴PD=CD•tan∠ACD=50

3

•tan60°=150（m）．
在Rt△PAB中，tan∠PBA=

PA

AB

，
∴PA=AB•tan∠PBA=30

3

•tan60°=90（m）．
∴S_{四边形ABCD}=S_△CDP-S_△ABP=

1

2

×50

3

×150-

1

2

×30

3

×90=2400

3

（m²）．
即这块土地的面积为2400

3

m²．