题目内容
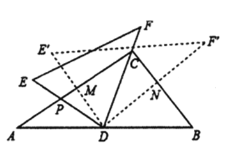
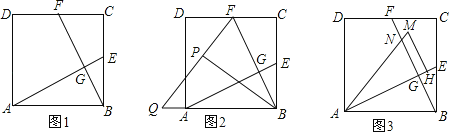
【题目】如图1,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF,交点为G.若正方形的边长为2.
(1)求证:AE⊥BF;
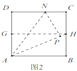
(2)将△BCF沿BF对折,得到△BPF(如图2),延长FP交BA的延长线于点Q,求AQ的长;
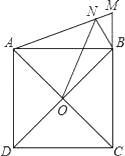
(3)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,求四边形MNGH的面积.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)运用Rt△ABE≌Rt△BCF,再利用角的关系求得∠BGE=90°即可;
(2)首先利用折叠的性质和平行线的性质得到QF=QB,然后在Rt△QPB中,利用勾股定理即可解决问题.
(3)首先证明△AGN∽△AHM,再根据面积比等于相似比的平方,求得S△AGN=![]() ,再利用S四边形GHMN=S△AHM﹣S△AGN求解.
,再利用S四边形GHMN=S△AHM﹣S△AGN求解.
(1)证明: ∵四边形ABCD是正方形,
![]() .
.
∵E,F分别是正方形ABCD边BC,CD的中点,
∴CF=BE.
在Rt△ABE和Rt△BCF中,
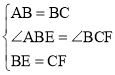 ,
,
∴Rt△ABE≌Rt△BCF(SAS),
∴∠BAE=∠CBF.
又∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠BGE=90°,
∴AE⊥BF.
(2)由折叠的性质得FP=FC,∠PFB=∠BFC,∠FPB=∠BCF =90°,
∵四边形ABCD是正方形,
![]() .
.
∴∠CFB=∠ABF,
∴∠ABF=∠PFB,
∴QF=QB.
∵PF=FC=1,PB=BC=2,
在Rt△BPQ中,设QB=x,
∴x2=(x﹣1)2+22,
∴x=![]() ,
,
∴AQ=BQ﹣AB=![]() .
.
(3)解:![]() ,
,
![]() .
.
由旋转的性质可知,![]() .
.
∵∠BAE=∠EAM,AE⊥BF,
∴AN=AB=2.
∵∠AHM=90°,
![]() .
.
![]() .
.
∴GN∥HM,
∴△AGN∽△AHM,
∴![]() =(
=(![]() )2.
)2.
![]() ,
,
∴![]() =(
=( ![]() )2,
)2,
∴S△AGN=![]() ,
,
∴S四边形GHMN=S△AHM﹣S△AGN=1﹣![]() =
=![]() ,
,
∴四边形GHMN的面积是 ![]() .
.

【题目】某运输公司现将一批152吨的货物运往A,B两地,若用大小货车15辆,则恰好能一次性运完这批货.已知这两种大小货车的载货能力分别为12吨/辆和8吨/辆,其运往A,B两地的运费如下表所示:
目的地(车型) | A地(元/辆) | B地(元/辆) |
大货车 | 800 | 900 |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆.(用二元一次方程组解答)
(2)现安排其中的10辆货车前往A地,其余货车前往B地,设前往A地的大货车为x辆,前往A,B两地总费用为w元,试求w与x的函数解析式.