题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 是
是![]() 上一点,经过
上一点,经过![]() ,
,![]() 两点的
两点的![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,作
,作![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
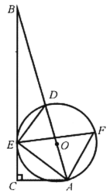
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)AC=6.4
【解析】
(1)连接OE,根据同圆的半径相等和角平分线可得:OE∥AC,则∠BEO=∠C=90°,解决问题;
(2)过A作AH⊥EF于H,根据三角函数先计算![]() ,证明△AEH是等腰直角三角形,则AE=
,证明△AEH是等腰直角三角形,则AE=![]() AH=8,证明△AED∽△ACE,得到
AH=8,证明△AED∽△ACE,得到![]() 即可解决问题.
即可解决问题.
证明:(1)连接OE,
∵OE=OA,
∴∠OEA=∠OAE,
∵AE平分∠BAC,
∴∠OAE=∠CAE,
∴∠CAE=∠OEA,
∴OE∥AC,
∴∠BEO=∠C=90°,
∴BC是⊙O的切线;
(2)过A作AH⊥EF于H,
![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵AD是⊙O的直径,
∴∠AED=90°,
∵EF平分∠AED,
∴∠AEF=45°,
∴△AEH是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴AC=6.4.

练习册系列答案
相关题目