题目内容
【题目】如图，在矩形ABCD中，AB=6，BC=
，E为CD边上一点，将△BCE沿BE折叠，点C的对应点为点F，连接AF，若
，则CE=__________．
【答案】
【解析】
已知
，可作辅助线构造直角三角形，设未知数，利用勾股定理可求出FM、BM，进而求出FN，再利用三角形相似和折叠的性质求出EC．
解：过点F作MN∥AD，交AB、CD分别于点M、N，则MN⊥AB，MN⊥CD，
∴∠FNE=∠BMF=90°
∴∠NFE+∠NEF=90°
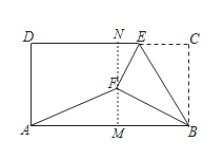
由折叠得：EC=EF，BC=BF=
，∠C=∠BFE=90°，
∴∠NFE+∠BFM=90°
∴∠MFB=∠NEF
∵
∴设FM=x，则AM=3x，
，
∴
在Rt△BFM中，由勾股定理得：
解得：
∵
∴x=1
∴FM=1，AM=BM=3，
∵∠FNE=∠BMF=90°, ∠MFB=∠NEF
∴△BMF∽△FNE，
∴
∴
∴EF=
故答案为：
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
【题目】某公司推出一款产品，经市场调查发现，该产品的日销售量y（个）与销售单价x（元）之间满足一次函数关系．关于销售单价，日销售量，日销售利润的几组对应值如下表：
销售单价x（元） | 85 | 95 | 105 | 115 |
日销售量y（个） | 175 | 125 | 75 | m |
日销售利润w（元） | 875 | 1875 | 1875 | 875 |
（注：日销售利润=日销售量×（销售单价﹣成本单价））
（1）求y关于x的函数解析式（不要求写出x的取值范围）及m的值；
（2）根据以上信息，填空：
该产品的成本单价是 元，当销售单价x= 元时，日销售利润w最大，最大值是 元；
（3）公司计划开展科技创新，以降低该产品的成本，预计在今后的销售中，日销售量与销售单价仍存在（1）中的关系．若想实现销售单价为90元时，日销售利润不低于3750元的销售目标，该产品的成本单价应不超过多少元？
