Question

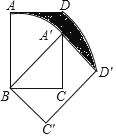
【题目】如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③AG∥CF；④S△FGC=3．其中正确结论的是_____．

Answer 1

【答案】①②③

【解析】

根据翻折变换的性质和正方形的性质可证Rt△ABG≌Rt△AFG；在直角△ECG中，根据勾股定理可证BG=GC；通过证明∠AGB=∠AGF=∠GFC=∠GCF，由平行线的判定可得AG∥CF；由于S△FGC=S△GCE-S△FEC，求得面积比较即可．

①正确．
理由：
∵AB=AD=AF，AG=AG，∠B=∠AFG=90°，

∴Rt△ABG≌Rt△AFG（HL）；

②正确．

理由：

EF=DE=CD=2，设BG=FG=x，则CG=6-x．

在直角△ECG中，根据勾股定理，得（6-x）2+42=（x+2）2，

解得x=3．

∴BG=3=6-3=GC；

③正确．

理由：

∵CG=BG，BG=GF，

∴CG=GF，

∴△FGC是等腰三角形，∠GFC=∠GCF．

又∵Rt△ABG≌Rt△AFG；

∴∠AGB=∠AGF，∠AGB+∠AGF=2∠AGB=180°-∠FGC=∠GFC+∠GCF=2∠GFC=2∠GCF，

∴∠AGB=∠AGF=∠GFC=∠GCF，

∴AG∥CF；

④错误．

理由：

∵S△GCE=GCCE=×3×4=6
∵GF=3，EF=2，△GFC和△FCE等高，
∴S△GFC：S△FCE=3：2，
∴S△GFC=×6=≠3．
故④不正确．

∴正确的个数有3个: ①②③.

故答案为：①②③