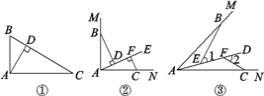题目内容
【题目】如图,已知正方形ABCD,点E在CB的延长线上,联结AE、DE,DE与边AB交于点F,FG∥BE且与AE交于点G. 
(1)求证:GF=BF.
(2)在BC边上取点M,使得BM=BE,联结AM交DE于点O.求证:FOED=ODEF.
【答案】
(1)证明:∵四边形ABCD是正方形,
∴AD∥BC,AB∥CD,AD=CD,
∵GF∥BE,
∴GF∥BC,
∴GF∥AD,
∴ ![]() ,
,
∵AB∥CD,
∴ ![]() ,
,
∵AD=CD,
∴GF=BF
(2)证明:延长GF交AM于H,
∵GF∥BC,
∴FH∥BC,
∴ ![]() ,
,
∴ ![]() ,
,
∵BM=BE,
∴GF=FH,
∵GF∥AD,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴FOED=ODEF
【解析】(1)根据已知条件可得到GF∥AD,则有 ![]() ,由BF∥CD可得到
,由BF∥CD可得到 ![]() ,又因为AD=CD,可得到GF=FB;(2)延长GF交AM于H,根据平行线分线段成比例定理得到
,又因为AD=CD,可得到GF=FB;(2)延长GF交AM于H,根据平行线分线段成比例定理得到 ![]() ,由于BM=BE,得到GF=FH,由GF∥AD,得到
,由于BM=BE,得到GF=FH,由GF∥AD,得到 ![]() ,等量代换得到
,等量代换得到 ![]() ,即
,即 ![]() ,于是得到结论.
,于是得到结论.

练习册系列答案
相关题目
【题目】“表1”为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
成绩(分) | 70 | 80 | 90 |
男生(人) | 5 | 10 | 7 |
女生(人) | 4 | 13 | 4 |
A.男生的平均成绩大于女生的平均成绩
B.男生的平均成绩小于女生的平均成绩
C.男生成绩的中位数大于女生成绩的中位数
D.男生成绩的中位数小于女生成绩的中位数