题目内容
【题目】
(1)解不等式组: 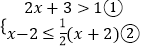
(2)解方程: ![]() =
= ![]() .
.
【答案】
(1)解①得:x>﹣1,
解②得:x≤6,
故不等式组的解集为:﹣1<x≤6
(2)由题意可得:5(x+2)=3(2x﹣1),
解得:x=13,
检验:当x=13时,(x+2)≠0,2x﹣1≠0,
故x=13是原方程的解
【解析】(1)分别解不等式,进而得出不等式组的解集;(2)直接利用分式的性质求出x的值,进而得出答案.
【考点精析】掌握去分母法和一元一次不等式组的解法是解答本题的根本,需要知道先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).

【题目】有这样一个问题:探究函数y=![]() 的图象与性质.小美根据学习函数的经验,对函数y=
的图象与性质.小美根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究下面是小美的探究过程,请补充完整:
的图象与性质进行了探究下面是小美的探究过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | -2 | - | -1 | - |
|
| 1 | 2 | 3 | 4 | … |
y | 0 | - | -1 | - |
|
| td style="width:28.95pt; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">m |
|
| … |
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)结合函数的图象,写出该函数的一条性质: .
【题目】雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康,太原市会持续出现雾霾天气吗?在2016年2月周末休息期间,某校九年级1班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计图表,观察并回答下列问题:
类别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 | m |
C | 城中村燃煤问题 | 15% |
D | 其他(绿化不足等) | n |
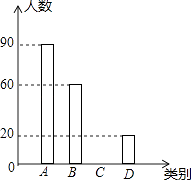
(1)请你求出本次被调查市民的人数及m,n的值,并补全条形统计图;
(2)若太原市有300万人口,请你估计持有A,B两类看法的市民共有多少人?
(3)学校要求小颖同学在A,B,C,D这四个雾霾天气的主要成因中,随机抽取两项作为课题研究的项目进行考察分析,请用画树状图或列表的方法,求出小颖同学刚好抽到B(汽车尾气排放),C(城中村燃煤问题)的概率.(用A,B,C,D表示各项目)