Question

【题目】如图，在△ABC中，AB=AC，∠BAC=90°，点P是BC上的一动点，AP=AQ，∠PAQ=90°，连接CQ．

(1)求证：CQ⊥BC．

(2)△ACQ能否是直角三角形？若能，请直接写出此时点P的位置；若不能，请说明理由.

(3)当点P在BC上什么位置时，△ACQ是等腰三角形？请说明理由．

Answer 1

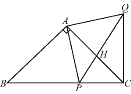
【答案】（1）证明见解析；（2）点P为BC的中点或与点C重合时，△ACQ是直角三角形；（3）当点P为BC的中点或与点C重合或BP=AB时，△ACQ是等腰三角形.

【解析】

（1）根据同角的余角相等求出∠BAP=∠CAQ，然后利用“边角边”证明△ABP和△ACQ全等，根据全等三角形对应角相等可得∠ACQ=∠B，再根据等腰直角三角形的性质得到∠B=∠ACB=45°，然后求出∠BCQ=90°，然后根据垂直的定义证明即可；
（2）分∠APB和∠BAP是直角两种情况求出点P的位置，再根据△ABP和△ACQ全等解答；
（3）分BP=AB，AB=AP，AP=BP三种情况讨论求出点P的位置，再根据△ABP和△ACQ全等解答．

解：（1）∵∠BAP+∠CAP=∠BAC=90°,∠CAQ+∠CAP=∠PAQ=90°,

∴∠BAP=∠CAQ,

在△ABP和△ACQ中，

，

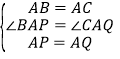∴△ABP≌△ACQ(SAS),

∴∠ACQ=∠B,

∵AB=AC,∠BAC=90°,

∴∠B=∠ACB=45°,

∴∠BCQ=∠ACB+∠ACQ=45°+45°=90°,

∴CQ⊥BC；

（2）当点P为BC的中点或与点C重合时，△ACQ是直角三角形；

（3）①当BP=AB时，△ABP是等腰三角形;

②当AB=AP时，点P与点C重合;

③当AP=BP时,点P为BC的中点；

∵△ABP≌△ACQ,

∴当点P为BC的中点或与点C重合或BP=AB时，△ACQ是等腰三角形.