��Ŀ����
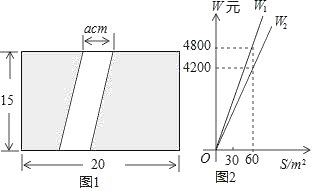
����Ŀ����ͼ1��Ϊ����У������ijУ�ƻ���һ�鳤Ϊ20m����Ϊ15m�ij����οյ�����һ����Ϊa��m�����������µIJ��������ƺ�����̵أ�
��1���������Ϊ�� ��m2���̵ص����Ϊ�� ��m2���ú�a�Ĵ���ʽ��ʾ����
��2����֪ij����˾�������̵ص����W1��Ԫ����W2��Ԫ���������S֮��ĺ�����ϵ��ͼ2��ʾ�����ֹ�˾��һƽ���������̵ص���۷ֱ�Ϊ�� ��Ԫ���� ��Ԫ����ֱ��д�����������W1��Ԫ�������̵ص����W2��Ԫ����a��m���Ĺ�ϵʽ�������ѧУ�����ɸù�˾�н�����Ŀ����Ҫ�����������Ȳ�����2m�Ҳ�����5m����ô����Ϊ����ʱ�����������̵ص��������ͣ���������Ϊ����Ԫ��
���𰸡���1��15a����300��15a������2���٢�80��70������W1��80��15a��1200a��W2��70��300��15a������1050a+21000��������Ϊ2��ʱ�����������̵ص��������ͣ���������Ϊ21300Ԫ��
��������
��1������ͼ�μ�����⣻
��2�����ֹ�˾��һƽ���������̵ص���۷ֱ�Ϊ![]() ��80Ԫ��
��80Ԫ��![]() ��70Ԫ�ڸ������⼴���г���ϵʽ����W��W1+W2��1200a+����1050a+21000����150a+21000���ٸ���2��a��5�����ɽ������.
��70Ԫ�ڸ������⼴���г���ϵʽ����W��W1+W2��1200a+����1050a+21000����150a+21000���ٸ���2��a��5�����ɽ������.
�⣺��1���������Ϊ15am2���̵ص����Ϊ��300��15a��m2��
�ʴ�Ϊ��15a����300��15a����
��2�����ֹ�˾��һƽ���������̵ص���۷ֱ�Ϊ![]() ��80Ԫ��
��80Ԫ��![]() ��70Ԫ��
��70Ԫ��
��W1��80��15a��1200a��
W2��70��300��15a������1050a+21000��
�����������Ŀ���ܷ���ΪWԪ��
��W��W1+W2��1200a+����1050a+21000����150a+21000��
��k��0��
��W��a�����������
��2��a��5��
�൱a��2ʱ��W����Сֵ��W��Сֵ��150��2+21000��21300��
������Ϊ2��ʱ�����������̵ص��������ͣ���������Ϊ21300Ԫ��
�ʴ�Ϊ����80��70��

����Ŀ��ij�ּ�ʱ��������0��00ʱ�̵�ȼ����������ʣ��ij���h��cm����ȼ�յ�ʱ��x��h��֮����һ�κ�����ϵ��h��x��һ���Ӧ��ֵ�����ʾ��
ȼ�յ�ʱ��x��h�� | �� | 3 | 4 | 5 | 6 | �� |
ʣ��ij���h��cm�� | �� | 210 | 200 | 190 | 180 | �� |
��1��д����������0��00ʱ�̵�Ȼ����ʣ��ij���h��cm����ȼ��ʱ��x��h���ĺ�����ϵʽ�������ͺ�������ʽ��x��ϵ�����������ʵ�����壻
��2��ͨ������˵����������ʣ��ij���Ϊ125cmʱ��ʱ�̣�