题目内容
【题目】已知在数轴上 A,B 两点对应数分别为﹣4,20.
(1)若 P 点为线段 AB 的中点,求 P 点对应的数.
(2)若点 A、点 B 同时分别以 2 个单位长度/秒的速度相向运动,点 M(M 点在原点)同时以 4 个单位长度/秒的速度向右运动.几秒后点 M 到点 A、点 B 的距离相等?求此时 M 对应的数.
(3)在(2)的条件下,是否存在 M 点,使 3MA=2MB?若存在,求出点 M 对应的数;若不存在,请说明理由.
【答案】(1)8;(2)t=2,M表示8或t=6,M表示24;(3)![]() 或
或![]() .
.
【解析】
(1)利用中点坐标计算方法直接得出答案即可;
(2)画出图形,设x秒后点M到点A、点B的距离相等,分别表示出AM和BM的长度,建立方程求得答案即可;
(3)利用(2)中的AM和BM的长度,分两种情况:M在AB之间,A在BM之间,结合3MA=2MB建立方程求得答案即可.
解:(1)P点表示的数是![]() ;
;
(2)如图,

设x秒后点M到点A、点B的距离相等,
AM=4t-(-4+2t)=2t+4,BM=20-2t-4t=20-6t,
则2t+4=20-6t,
解得t=2,
M表示2×4=8.
A、B重合时,MA=BM,此时t=6,此时M表示24.
(3)如图①,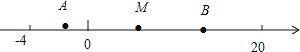
AM=4t-(-4+2t)=2t+4,BM=20-2t-4t=20-6t,
∵3MA=2MB,
∴3(2t+4)=2(20-6t),
![]() ,
,
∴点M表示![]() ,
,
如图②,![]()
AM=4t-(-4+2t)=2t+4,BM=2t+4t-20=6t-20,
∵3MA=2MB,
∴3(2t+4)=2(6t-20),
![]()
∴点M表示![]()

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目