题目内容
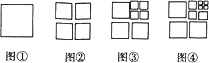
【题目】将图①中的正方形剪开得到图②，图②中共有4个正方形；将图②中一个正方形剪开得到图③，图③中共有7个正方形；将图③中一个正方形剪开得到图④，图④中共有10个正方形…，如此下去，则第2014个图中共有正方形的个数为( )
A. 2014. B. 2017 C. 6040 D. 6044
【答案】C
【解析】试题分析：观察图形可知，每剪开一次多出3个正方形，然后写出前4个图形中正方形的个数，再根据此规律写出第n个图形中的正方形的个数的表达式，再代入2014求得问题即可．
解：第1个图形有正方形1个，
第2个图形有正方形4个，
第3个图形有正方形7个，
第4个图形有正方形10个，
…，
第n个图形有正方形(3n2)个.
则第2014个图中共有正方形的个数为3×20142=6040.
故选：C.
练习册系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
