题目内容
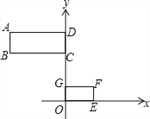
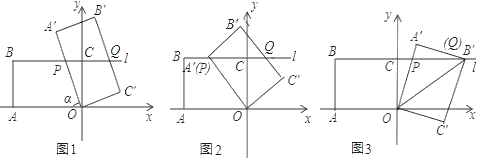
【题目】如图1,在平面直角坐标系中,O为坐标原点,点A(﹣4,0),直线l∥x轴,交y轴于点C(0,3),点B(﹣4,3)在直线l上,将矩形OABC绕点O按顺时针方向旋转α度,得到矩形OA′B′C′,此时直线OA′、B′C′分别与直线l相交于点P、Q.
(1)当α=90°时,点B′的坐标为 .
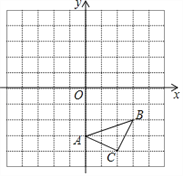
(2)如图2,当点A′落在l上时,点P的坐标为 ;
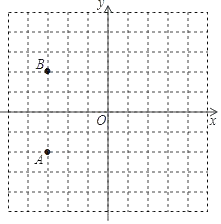
(3)如图3,当矩形OA′B′C′的顶点B′落在l上时.
①求OP的长度;②S△OPB′的值是 .
(4)在矩形OABC旋转的过程中(旋转角0°<α≤180°),以O,P,B′,Q为顶点的四边形能否成为平行四边形?如果能,请直接写出点B′和点P的坐标;如果不能,请简要说明理由.
【答案】(1)(3,4);(2)(﹣![]() ,3);(3)①OP=
,3);(3)①OP=![]() ;②
;②![]() ;(4)在矩形OABC旋转的过程中(旋转角0°<α≤180°),以O,P,B′,Q为顶点的四边形能成为平行四边形,此时点B′的坐标为(5,0),点P的坐标为(4,3).
;(4)在矩形OABC旋转的过程中(旋转角0°<α≤180°),以O,P,B′,Q为顶点的四边形能成为平行四边形,此时点B′的坐标为(5,0),点P的坐标为(4,3).
【解析】
(1)根据旋转的得到B′的坐标;
(2)根据在Rt△OCA′,利用勾股定理即可求解;
(3)①根据已知条件得到△CPO≌△A′PB′,设OP=x,则CP=A′P=4﹣x,在Rt△CPO中,利用OP2=OC2+CP2,即x2=(4﹣x)2+32即可求出x的值,即可求解;②根据S△OPB′=![]() PB′OC即可求解;
PB′OC即可求解;
(4)当点B′落在x轴上时,由OB′∥PQ,OP∥B′Q,此时四边形OPQB′为平行四边形,再根据平行四边形的性质即可求解.
解:(1)∵A(﹣4,0),B(﹣4,3),
∴OA=4,AB=3.
由旋转的性质,可知:OA′=OA=4,A′B′=AB=3,
∴当α=90°时,点B′的坐标为(3,4).
故答案为:(3,4).
(2)在Rt△OCA′中,OA′=4,OC=3,
∴A′C=![]() =
=![]() ,
,
∴当点A′落在l上时,点P的坐标为(﹣![]() ,3).
,3).
故答案为:(﹣![]() ,3).
,3).
(3)①当四边形OA′B′C′的顶点B′落在BC的延长线上时,
在△CPO和△A′PB′中,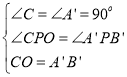 ,
,
∴△CPO≌△A′PB′(AAS),
∴OP=B′P,CP=A′P.
设OP=x,则CP=A′P=4﹣x.
在Rt△CPO中,OP=x,CP=4﹣x,OC=3,
∴OP2=OC2+CP2,即x2=(4﹣x)2+32,
解得:x=![]() ,
,
∴OP=![]() .
.
②∵B′P=OP=![]() ,
,
∴S△OPB′=![]() PB′OC=
PB′OC=![]() ×
×![]() ×3=
×3=![]() .
.
故答案为:![]() .
.
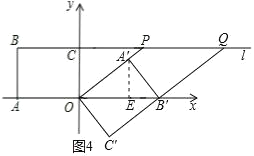
(4)当点B′落在x轴上时,∵OB′∥PQ,OP∥B′Q,
∴此时四边形OPQB′为平行四边形.
过点A′作A′E⊥x轴于点E,如图4所示.
∵OA′=4,A′B′=3,
∴OB′=![]() =5,A′E=
=5,A′E=![]() =
=![]() ,OE=
,OE=![]() =
=![]() ,
,
∴点B′的坐标为(5,0),点A′的坐标为(![]() ,
,![]() ).
).
设直线OA′的解析式为y=kx(k≠0),
将A′(![]() ,
,![]() )代入y=kx,得:
)代入y=kx,得:
![]() =
=![]() k,解得:k=
k,解得:k=![]() ,
,
∴直线OA′的解析式为y=![]() x.
x.
当y=3时,有![]() x=3,
x=3,
解得:x=4,
∴点P的坐标为(4,3).
∴在矩形OABC旋转的过程中(旋转角0°<α≤180°),以O,P,B′,Q为顶点的四边形能成为平行四边形,此时点B′的坐标为(5,0),点P的坐标为(4,3).

 快乐5加2金卷系列答案
快乐5加2金卷系列答案【题目】“十·一”黄金周期间,武汉动物园在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)若9月30日的游客人数记为![]() ,请用
,请用![]() 的代数式表示10月2日的游客人数?
的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由。
(3)若9月30日的游客人数为2万人,门票每人10元。问黄金周期间武汉动物园门票收入是多少元?
【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱.各种品牌的山地车相继投放市场.顺风车行经营的![]() 型车2018年6月份销售总额为
型车2018年6月份销售总额为![]() 万元,今年经过改造升级后
万元,今年经过改造升级后![]() 型车每辆销售价比去年增加
型车每辆销售价比去年增加![]() 元,若今年6月份与去年6月份卖出的
元,若今年6月份与去年6月份卖出的![]() 型车数量相同,则今年6月份
型车数量相同,则今年6月份![]() 型车销售总额将比去年6月份销售总额增加
型车销售总额将比去年6月份销售总额增加![]() .
.
(1)今年6月份![]() 型车每辆售价多少元?(用列方程的方法解答)
型车每辆售价多少元?(用列方程的方法解答)
(2)已知![]() 两种型号车今年的进货及销售价格如下表:
两种型号车今年的进货及销售价格如下表:
|
| |
进货价格(元/辆) |
|
|
销售价格(元/辆) | 今年的销售价格 |
|
该车行计划7月份进这批![]() 型车和
型车和![]() 型车共
型车共![]() 辆,且
辆,且![]() 型车的进货数量不超过
型车的进货数量不超过![]() 型车数量的两倍,应如何进货才能是这批车获利最多?
型车数量的两倍,应如何进货才能是这批车获利最多?