Question

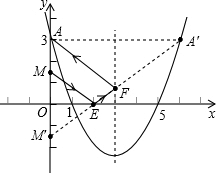
已知抛物线y=ax²+bx+c与y轴交于点A（0，3），与x轴交于（1，0）（5，0）两点，若一个动点P自OA的中点M出发，先到达x轴上的某点E，再到达抛物线的对称轴上某点F，最后运动到点A，则使点P运动的总路径最短的点E、点F的坐标分别是：E______，F______．

Answer 1

如图，∵抛物线与x轴交于（1，0）（5，0）两点，
∴抛物线的对称轴为直线x=

1+5

2

=3，
∴点A（0，3）关于直线x=3的对称点A′为（6，3），
又∵OA的中点M为（0，

3

2

），
∴点M关于x轴的对称点M′为（0，-

3

2

），
连接A′M′与x轴的交点、与对称轴的交点即为所求的点E、F，
设直线A′M′的解析式为y=kx+b，
则

6k+b=3 b=- 3 2

，
解得

k= 3 4 b=- 3 2

，
所以，直线A′M′的解析式为y=

3

4

x-

3

2

，
令y=0，则

3

4

x-

3

2

=0，
解得x=2，
令x=3，则y=

3

4

×3-

3

2

=

3

4

，
所以，点E（2，0），F（3，

3

4

）．
故答案为：E（2，0）；（3，

3

4

）．