题目内容

已知直线y=-2x+3与抛物线y=x2相交于A、B两点，O为坐标原点，那么△OAB的面积等于______．
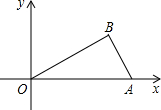
如图，直线y=-2x+3与抛物线y=x2相交，
即x2=-2x+3，
解得x1=1，x2=-3，
因此交点坐标为A为（1，1），B为（-3，9），
作AA1，BB1分别垂直于x轴，垂足为A1，B1，
∴S△OAB=S梯形AA1B1B-S△AA1O-S△BB1O，
=
1
2
×（1+9）×（1+3）-
1
2
×1×1-
1
2
×9×3，
=6．
故填6．
练习册系列答案
相关题目
如图，临沂三河口大桥有一段抛物线行的工桥梁，抛物线的表达式为y=ax2+bx，小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC，当小强骑自行车行驶10秒时和20秒时拱梁的高度相同，则小强骑自行车通过拱梁部分的桥面OC共需______秒．
如图，已知点O为坐标原点，∠AOB=30°，∠B=90°，且点A的坐标为（2，0）．
（1）求点B的坐标；
（2）若二次函数y=ax2+bx+c的图象经过A，B，O三点，求此二次函数的解析式；
（3）在（2）中的二次函数图象的OB段（不包括O，B点）上，是否存在一点C，使得四边形ABCO的面积最大？若存在，求出点C的坐标及四边形ABCO的最大面积；若不存在，请说明理由．
如图是某河上一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状，抛物线两端点与水面的距离都是1m，拱桥的跨度为10m，桥洞与水面的最大距离是5m，桥洞两侧壁上各有一盏距离水面4m的景观灯．若把拱桥的截面图放在平面直角坐标系中，则两盏景观灯之间的水平距离是（　　）
A．3mB．4mC．5mD．6m
如图，已知抛物线与x轴交于A（-1，0），B（3，0）两点，与y轴交于点C（0，3）．
（1）求抛物线的解析式；
（2）设抛物线的顶点为D，在其对称轴的右侧的抛物线上是否存在点P，使得△PDC是等腰三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由；
（3）点M是抛物线上一点，以B，C，D，M为顶点的四边形是直角梯形，试求出点M的坐标．
如图1，抛物线y=-
2
3
x2+bx+c与x轴相交于点A，C，与y轴相交于点B，连接AB，BC，点A的坐标为（2，0），tan∠BAO=2，以线段BC为直径作⊙M交AB与点D，过点B作直线l∥AC，与抛物线和⊙M的另一个交点分别是E，F．
（1）求该抛物线的函数表达式；
（2）求点C的坐标和线段EF的长；
（3）如图2，连接CD并延长，交直线l于点N，点P，Q为射线NB上的两个动点（点P在点Q的右侧，且不与N重合），线段PQ与EF的长度相等，连接DP，CQ，四边形CDPQ的周长是否有最小值？若有，请求出此时点P的坐标并直接写出四边形CDPQ周长的最小值；若没有，请说明理由．
已知抛物线y=ax2+bx+c与y轴交于点A（0，3），与x轴交于（1，0）（5，0）两点，若一个动点P自OA的中点M出发，先到达x轴上的某点E，再到达抛物线的对称轴上某点F，最后运动到点A，则使点P运动的总路径最短的点E、点F的坐标分别是：E______，F______．
蔬菜基地种植某种蔬菜，由市场行情分析知，1月份至6月份这种蔬菜的上市时间x（月份）与市场售价p（元/千克）的关系如下表：
上市时间x（月份）123456
市场售价p（元/千克）10.597.564.53
这种蔬菜每千克的种植成本y（元/千克）与上市时间x（月份）满足一个函数关系，这个函数的图象是抛物线的一段（如图）．

（1）写出上表中表示的市场售价p（元/千克）关于上市时间x（月份）的函数关系式______；
（2）若图中抛物线过A，B，C点，写出抛物线对应的函数关系式______；
（3）由以上信息分析，______月份上市出售这种蔬菜每千克的收益最大，最大值为______元（收益=市场售价一种植成本）．
有一种螃蟹，从海上捕获后不放养，最多只能存活两天．如果放养在塘内，可以延长存活时间，但每天也有一定数量的蟹死去．假设放养期内蟹的个体质量基本保持不变，现有一经销商，按市场价收购这种活蟹1000kg放养在塘内，此时市场价为每千克30元，据测算，此后每千克活蟹的市场价每天可上升1元，但是，放养一天需支出各种费用为400元，且平均每天还有10kg蟹死去，假定死蟹均于当天全部销售出，售价都是每千克20元．
（1）设x天后每千克活蟹的市场价为p元，写出p关于x的函数关系式；
（2）如果放养x天后将活蟹一次性出售，并记1000kg蟹的销售总额为Q元，写出Q关于x的函数关系式；
（3）该经销商将这批蟹放养多少天后出售，可获最大利润（利润=Q-收购总额）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网