题目内容
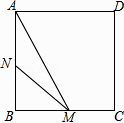
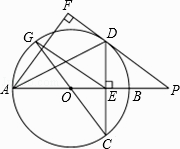
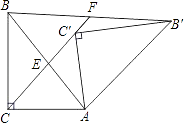
【题目】如图,在菱形ABCD中,CE⊥AB交AB延长线于点E,点F为点B关于CE的对称点,连接CF,分别延长DC,CF至点G,H,使FH=CG,连接AG,DH交于点P.
(1)依题意补全图1;
(2)猜想AG和DH的数量关系并证明;
(3)若∠DAB=70°,是否存在点G,使得△ADP为等边三角形?若存在,求出CG的长;若不存在,说明理由.


【答案】(1)见解析;(2) AG=DH,理由见解析;(3) 不存在.理由见解析.
【解析】(1)依题意画图;
(2)根据菱形性质得![]() ,
,![]() ∥
∥![]() ,
,![]() ;由点
;由点![]() 为点
为点![]() 关于
关于![]() 的对称点,得
的对称点,得![]() 垂直平分
垂直平分![]() ,故
,故![]() ,
,![]() ,所以
,所以![]() ,再证
,再证![]() ,
,
由![]() ,
,![]() ,得
,得![]() .可证△
.可证△![]() ≌△
≌△![]() .
.
(3)由(2)可知,∠DAG=∠CDH,∠G=∠GAB,
证得∠DPA=∠PDG+∠G=∠DAG+∠GAB=70°>60°,故△ADP不可能是等边三角形.
(1)补全的图形,如图所示.

(2)AG=DH.
证明:∵四边形ABCD是菱形,
∴![]() ,
,![]() ∥
∥![]() ,
,![]() .
.
∵点![]() 为点
为点![]() 关于
关于![]() 的对称点,
的对称点,
∴![]() 垂直平分
垂直平分![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴△![]() ≌△
≌△![]() .
.
∴![]() .
.
(3)不存在.
理由如下:
由(2)可知,∠DAG=∠CDH,∠G=∠GAB,
∴∠DPA=∠PDG+∠G=∠DAG+∠GAB=70°>60°.
∴△ADP不可能是等边三角形.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案【题目】如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,…,称为“三角形数”;把1、4、9、16,25,…称为“正方形数”.同样的,可以把数1,5,12,22,…,等数称为“五边形数”.

将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
三角形数 | 1 | 3 | 6 | 10 | 15 | 21 | a | … |
正方形数 | 1 | 4 | 9 | 16 | 25 | b | 49 | … |
五边形数 | 1 | 5 | 12 | 22 | c | 51 | 70 | … |
(1)按照规律,表格中a= ,b= ,c= .
(2)观察表中规律,第n个“正方形数”是 ;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是 .