题目内容
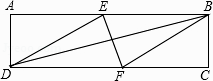
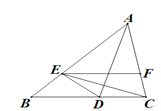
【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E,连接AG.
(1)求证:AG=CG;
(2)求证:AG2=GE·GF.

【答案】(1)证明见解析 (2)证明见解析
【解析】试题分析:
(1)由菱形的性质易证△ADG≌△CDG,从而可得AG=CG;
(2)由△ADG≌△CDG可得∠EAG=∠DCG,再由AB∥CD可得∠F=∠DCG,从而可得∠F=∠EAG,再利用∠AGE是公共角可证△AGE∽△FGA就可得到![]() ,所以
,所以![]()
试题解析:
(1)∵四边形ABCD是菱形,
∴AD=CD,∠ADB=∠CDB,
在△ADG与△CDG中, 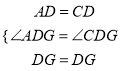 ,
,
∴△ADG≌△CDG,
∴AG=CG.
(2) ∵在菱形ABCD中,AB∥CD,
∴∠F=∠GCD.
∵△ADG≌△CDG,
∴∠EAG=∠DCG,
∴∠EAG=∠F.
又∵∠AGE=∠FGA,
∴△AGE∽△FGA,
∴![]() ,
,
∴AG2=GE·GF.

练习册系列答案
相关题目