题目内容
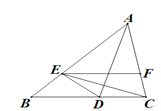
【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E. 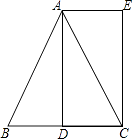
(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.
【答案】
(1)证明:∵AB=AC,
∴∠B=∠ACD,
∵AE∥BC,
∴∠EAC=∠ACD,
∴∠B=∠EAC,
∵AD是BC边上的中线,
∴AD⊥BC,
∵CE⊥AE,
∴∠ADC=∠CEA=90°
在△ABD和△CAE中

∴△ABD≌△CAE(AAS);
(2)证明:AB=DE,AB∥DE,如图所示,
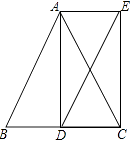
∵AD⊥BC,AE∥BC,
∴AD⊥AE,
又∵CE⊥AE,
∴四边形ADCE是矩形,
∴AC=DE,
∵AB=AC,
∴AB=DE.
∵AB=AC,
∴BD=DC,
∵四边形ADCE是矩形,
∴AE∥CD,AE=DC,
∴AE∥BD,AE=BD,
∴四边形ABDE是平行四边形,
∴AB∥DE且AB=DE.
【解析】(1)运用AAS证明△ABD≌△CAE;(2)易证四边形ADCE是矩形,所以AC=DE=AB,也可证四边形ABDE是平行四边形得到AB=DE.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目