题目内容
【题目】如图,直线y=﹣ ![]() x+m(m>0)与x轴交于点C,与y轴交于点D,以CD为边作矩形ANCD,点A在x轴上.双曲线y=
x+m(m>0)与x轴交于点C,与y轴交于点D,以CD为边作矩形ANCD,点A在x轴上.双曲线y= ![]() 经过点B,与直线CD交于点E,则点E的坐标为( )
经过点B,与直线CD交于点E,则点E的坐标为( ) 
A.( ![]() ,﹣
,﹣ ![]() )
)
B.(4,﹣ ![]() )
)
C.( ![]() ,﹣
,﹣ ![]() )
)
D.(6,﹣1)
【答案】D
【解析】解:根据题意,直线y=﹣ ![]() x+m与x轴交于C,与y轴交于D, 分别令x=0,y=0,
x+m与x轴交于C,与y轴交于D, 分别令x=0,y=0,
得y=m,x=2m,
即D(0,m),C(2m,0),
又AD⊥DC且过点D,
所以直线AD所在函数解析式为:y=2x+m,
令y=0,得x=﹣ ![]() m,
m,
即A(﹣ ![]() m,0),
m,0),
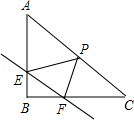
作BH⊥AC于H,
∵四边形ABCD是矩形,
∴AD=BC,∠DAO=∠BCH,
在△AOD和△CHB中
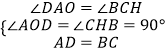
∴△AOD≌△CHB(AAS),
∴BH=OD=m,CH=OA= ![]() m,
m,
∴OH= ![]() m,
m,
∴B点的坐标为B( ![]() m,﹣m)
m,﹣m)
又B在双曲线双曲线y= ![]() (k<0)上,
(k<0)上,
∴ ![]() m(﹣m)=﹣6,
m(﹣m)=﹣6,
解得m=±2,
∵m>0,
∴m=2,
∴直线CD的解析式为y=﹣ ![]() x+2,
x+2,
解 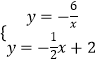 ,
,
得 ![]() 和
和 ![]() ,
,
故点E的坐标为(6,﹣1),
故选D.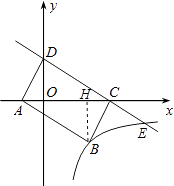

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某兴趣小组10名学生在一次数学测试中的成绩如表(满分150分)
分数(单位:分) | 105 | 130 | 140 | 150 |
人数(单位:人) | 2 | 4 | 3 | 1 |
下列说法中,不正确的是( )
A.这组数据的众数是130
B.这组数据的中位数是130
C.这组数据的平均数是130
D.这组数据的方差是112.5