Question

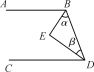
【题目】如图所示，已知等腰三角形ABC的底边BC=20cm，D是腰AB上一点，且CD=16cm，BD=12cm，求△ABC的周长．

Answer 1

【答案】53

【解析】试题分析：

由BC=20、CD=16、BD=12由勾股定理逆定理易证∠BDC=90°，再设AD=x，则AC=AB=AD+BD=12+x，在Rt△ACD中由勾股定理建立方程，解出x的值，即可求得△ABC的周长了.

试题解析：

设AD=xcm ,

∵BD2+CD2=122+162=400，BC2=202=400，

∴BD2+CD2=BC2 ，

∴△BDC是直角三角形，

∴∠BDC=900 ，∠ADC=900 ，

∴在 Rt△ACD中：AD2+CD2 =AC2 ，

∴x2+162=(x+12)2，解得：x=

∴AB=AC=12+=

∴△ABC的周长=AB+AC+BC=++20=.