题目内容
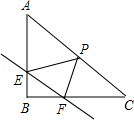
【题目】如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB= ![]() ,BC=
,BC= ![]() .
.
(1)当E、F均为两直角边的中点时,求证:四边形EPFB是矩形,并求出此时EF的长;
(2)设EF的长度为x(x>0),当∠EPF=∠A时,用含x的代数式表示EP的长;
(3)设△PEF的面积为S,则当EF为多少时,S有最大值,并求出该最大值.
【答案】
(1)
解:如图1,
∵E是AB的中点,P是AC的中点,
∴EP∥BC,且EP= ![]() BC,
BC,
∵F是BC的中点,
∴EP∥BF,且EP=BF,
四边形EPFB是平行四边形,
∵∠B=90°,
∴四边形EPFB是矩形
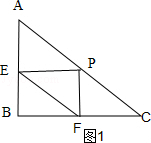
(2)
解:∵AB= ![]() ,BC=
,BC= ![]() .
.
∴BE= ![]() ,BF=
,BF= ![]() ,
,
∴EF= ![]() =1.(2)∵EF∥AC,
=1.(2)∵EF∥AC,
∴∠APE=∠PEF,∵∠EPF=∠A,
∴△APE∽△PEF.
∴ ![]() ,
,
∵AP=1,EF=x,
∴EP2=x,
∴EP= ![]()
(3)
解:如图2,作FH⊥AC交AC于点H,
∵EF∥AC,
∴△BEF∽△BAC,
设EF=x,则BF= ![]() x,CF=
x,CF= ![]() ﹣
﹣ ![]() x,
x,
∴FH= ![]() CF=
CF= ![]() ﹣
﹣ ![]() x,
x,
∴S= ![]() EFFH=﹣
EFFH=﹣ ![]() x2+
x2+ ![]() x=﹣
x=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
∴当x=1,即EF=1时,S有最大值为 ![]() .
.
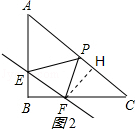
【解析】(1)先求出四边形EPFB是平行四边形,再由∠B=90°得出四边形EPFB是矩形,利用勾股定理求出EF.(2)证明△APE∽△PEF,得出对应边成比例,即可得出结果.(3)作FH⊥AC交AC于点H,设EF=x,得出BF,CF及FH的值,再利用三角形面积求出EF及最大值,利用中位线定理即可求出EP的值.

练习册系列答案
相关题目