Question

【题目】如图，矩形ABCD中，AB=6,AD=8，P、E分别是线段AC、BC上的点，且四边形PEFD是矩形，若△PCD是等腰三角形，求AP的长．

Answer 1

【答案】AP=4或AP=5或AP=

【解析】试题分析：先求出AC，再分三种情况讨论计算即可得出结论.

试题解析：在矩形ABCD中，AB=6，AD=8，∠ADC=90°，
∴DC=AB=6，
∴AC==10，
要使△PCD是等腰三角形，
①当CP=CD时，AP=AC-CP=10-6=4，
②当PD=PC时，∠PDC=∠PCD，
∵∠PCD+∠PAD=∠PDC+∠PDA=90°，
∴∠PAD=∠PDA，
∴PD=PA，
∴PA=PC，
∴AP=AC=5，
③当DP=DC时，如图1，过点D作DQ⊥AC于Q，则PQ=CQ，

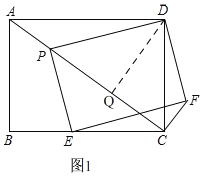
∵S△ADC=ADDC=ACDQ，
∴DQ=，
∴CQ=，
∴PC=2CQ=，
∴AP=AC-PC=10-=；
所以，若△PCD是等腰三角形时，AP=4或5或.