Question

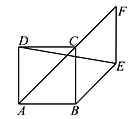
【题目】如图，四边形ABCD是正方形，AB=1，点F是对角线AC延长线上一点，以BC、CF为邻边作菱形BEFC，连接DE，则DE的长是（ ）．

A. B. C. D. 2

Answer 1

【答案】C

【解析】

延长DC交EF于G，则CG⊥EF，由正方形和菱形的性质得出∠FCG=∠ACD=45°，CD=BC=CF=EF=1，得出△CFG是等腰直角三角形，得出CG=FG，求出DG=CD+CG=1，GE=EF﹣FG=1．在Rt△DEG中，由勾股定理即可得出答案．

延长DC交EF于G，如图所示，则CG⊥EF，∴∠CGF=∠CGE=90°．

∵四边形ABCD是正方形，四边形BEFC是菱形，∴∠FCG=∠ACD=45°，CD=BC=CF=EF=1，∴△CFG是等腰直角三角形，∴CG=FGCF，∴DG=CD+CG=1，GE=EF﹣FG=1．在Rt△DEG中，由勾股定理得：DE．

故选C．