题目内容
【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E. 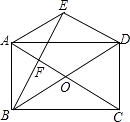
(1)求证:四边形AODE是菱形;
(2)连接BE,交AC于点F.若BE⊥ED于点E,求∠AOD的度数.
【答案】
(1)证明:∵AE∥BD,ED∥AC,
∴四边形AODE是平行四边形,
∵四边形ABCD是矩形,
∴OA=OC= ![]() AC,OB=OD=
AC,OB=OD= ![]() BD,AC=BD,
BD,AC=BD,
∴OA=OC=OD,
∴四边形AODE是菱形
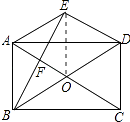
(2)解:连接OE,如图所示:
由(1)得:四边形AODE是菱形,
∴AE=OB=OA,
∵AE∥BD,
∴四边形AEOB是平行四边形,
∵BE⊥ED,ED∥AC,
∴BE⊥AC,
∴四边形AEOB是菱形,
∴AE=AB=OB,
∴AB=OB=OA,
∴△AOB是等边三角形,
∴∠AOB=60°,
∴∠AOD=180°﹣60°=120°.
【解析】(1)先证明四边形AODE是平行四边形,再由矩形的性质得出OA=OC=OD,即可得出四边形AODE是菱形;(2)连接OE,由菱形的性质得出AE=OB=OA,证明四边形AEOB是菱形,得出AB=OB=OA,证出△AOB是等边三角形,得出∠AOB=60°,再由平角的定义即可得出结果.
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目