题目内容
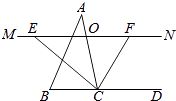
【题目】如图,在矩形ABCD中,AE平分∠BAD , ∠1=15°.
(1)求∠2的度数.
(2)求证:BO=BE .
【答案】
(1)
解答:解:∵在矩形ABCD中,AE平分∠BAD,∠1=15°,
∴∠AEB=∠EAD=45°,
∴∠2=∠AEB-∠1=30°.
(2)
解答:证明:由(1)可知∠2=30°,
∴∠BAO=60°,
∵OA=OB,
∴△OAB是等边三角形,
∴OB=AB,
∵∠AEB=∠EAD=∠BAE=45°,
∴AB=BE,
∴BO=BE.
【解析】(1)利用矩形的性质和角平分线的性质可知∠AEB=∠EAD=45°,那么∠2=∠AEB-∠1=30°;(2)通过∠2=30°,∠BAO=60°,证得△OAB是等边三角形,结合AB=BE可得BO=BE .
【考点精析】根据题目的已知条件,利用等边三角形的性质和矩形的性质的相关知识可以得到问题的答案,需要掌握等边三角形的三个角都相等并且每个角都是60°;矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
相关题目