Question

【题目】如图所示，直线a经过正方形ABCD的顶点A，分别过正方形的顶点B、D作BF⊥a于点F，DE⊥a于点E，若DE=8，BF=5，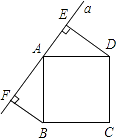

（1）求EF的长．
（2）求正方形ABCD的面积．

Answer 1

【答案】
（1）解：∵四边形ABCD是正方形，

∴AD=AB，∠BAD=90°，

∴D作BF⊥a于点F，DE⊥a于点E，

∴∠DEA=∠AFB=90°，

∴∠EDA+∠AED=90°，∠EAD+∠FAB=90°，

∴∠EDA=∠FAB，

在△AED和△BFA中

∴△AED≌△BFA（AAS），

∴AE=BF，AF=DE，

∵DE=8，BF=5，

∴AE=5，AF=8，

∴EF=AE+AF=8

（2）解：在Rt△AFB中，由勾股定理得：AB2=AF2+BF2=82+52=89，

即正方形ABCD的面积为89

【解析】（1）根据正方形的性质得出AD=AB，∠BAD=90°，根据垂直得出∠DEA=∠AFB=90°，求出∠EDA=∠FAB，根据AAS推出△AED≌△BFA，根据全等三角形的性质得出AE=BF=5，AF=DE=8，即可求出答案；（2）根据勾股定理求出AB2=AF2+BF2=89，即可得出答案．
【考点精析】解答此题的关键在于理解正方形的性质的相关知识，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．