��Ŀ����
����Ŀ��ij�߲˾�����ȥ�߲�������������ij���߲ˣ���֪�����߲˵���������20ǧ�ˡ�60ǧ��֮�䣨��20ǧ�˺�60ǧ�ˣ�ʱ��ÿǧ����������5Ԫ��������60ǧ��ʱ�������������߲�ȫ������ۣ�
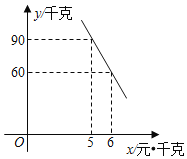
��1�������飬���߲˾��������۸����߲˵���������y��ǧ�ˣ������ۼ�x��Ԫ/ǧ�ˣ���һ�κ�����ϵ����ͼ����ͼ�����y��x֮��ĺ�����ϵʽ��
��2�������߲˾�����ÿ�����۴����߲˲�����75ǧ�ˣ��ҵ������ۼ۲��䣬��ô���ۼ۶�Ϊ����ʱ���þ��������۴����߲˵ĵ�����������������Ϊ����Ԫ��
���𰸡���1��y����30x+240����2�����ۼ۶�Ϊ5.5Ԫʱ�����տɻ����������������Ϊ112.5Ԫ
��������
��1�����ô���ϵ�������ѵ㣨5��90������6��60������һ�κ�������ʽ���������ϵ�����ɣ�
��2���赱�տɻ�����w��Ԫ���������ۼ�ΪxԪ�����ݵڣ�1���ʼ������г�����w��x�ĺ�����ϵʽ���ٸ��ݶ��κ�����ͼ������ʼ�ʵ�����壨��30x+240��75����x��5.5���ó����ֵ.
�⣺��1�����һ�κ�������ʽΪy��kx+b��k��0�����ѵ㣨5��90������6��60�����룬��
![]() ��
��
���![]() ��
��
�ʸ�һ�κ�������ʽΪ��y����30x+240��
��2���赱�տɻ�����w��Ԫ���������ۼ�ΪxԪ���ɣ�1��֪��
w������30x+240����x��5��0.8����-30x2+360x-960
=��30��x��6��2+120����30x+240��75����x��5.5��
��x��5.5ʱ�����տɻ����������������Ϊ112.5Ԫ��

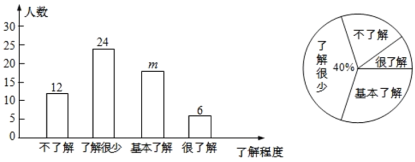
����Ŀ���������鸴ѧ��ѧУ��չ�˶�����ʽ�ķ���֪ʶ��������������ȫԱ�μӵ���������֪ʶ�������Ծ���Ŀ��10�⣬ÿ��10�֣��ֱַ�����꼶1,2,3���и������ȡ10��ͬѧ�ijɼ�����λ���֣���
�ռ������������£�
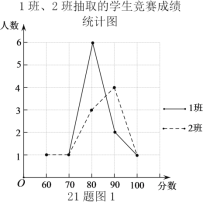
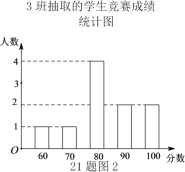
�������ݣ�
ƽ���� | ��λ�� | ���� | |
1�� | 83 |
| 80 |
2�� | 83 |
|
|
3�� |
| 80 | 80 |
����������Ϣ�ش��������⣺
��1����ֱ��д��������![]() ��
��![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
��2���Ƚ��������������ݵ�ƽ��������λ��������������Ϊ�ĸ���ijɼ��ȽϺã���˵�����ɣ�һ�����ɼ��ɣ���
��3��Ϊ����ѧ�����Ӱ�ȫ֪ʶ��ѧϰ��ѧУ���������ɼ����ֵ�ͬѧ�䷢��״����У���꼶ѧ����120�ˣ��Թ�����Ҫ�������Ž�״��