题目内容
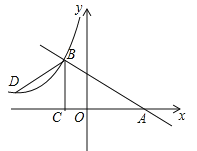
【题目】如图，在平面直角坐标系中，已知点
的坐标为
， 以为圆心，以
为半径的圆与
轴相交于点
，与
轴正半轴相交于点
过作
，点
为弦
上一点，连接
．
（1）求的长度；
（2）求证；直线
是⊙的切线；
（3）若点
是弧
上一动点(点与
点不重合)，过点的
的切线
交轴于
，若
为直角三角形，试求出所有符合条件的点的坐标．
【答案】（1）
；（2）见详解；（3）所有符合条件的点P的坐标是（-4，2），（4，2），（
，4），（
，4）．
【解析】
（1）根据勾股定理可以求得OB和OC的长度，从而可以得到B、C两点的坐标，即可得到答案；
（2）由
，∠AOC=90°，则∠OAE=90°，由MA为半径，则AE是切线；
（3）根据题意，画出相应的图形，然后利用分类讨论的方法可以得到点P的坐标．
解：（1）连接MB、MC，如图一所示，
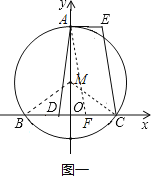
∵点M的坐标为（0，2），以M为圆心，以4为半径的圆与x轴相交于点B、C，
∴MB=MC=4，OM=2，
∵∠MOB=∠MOC=90°，
∴OB=
，
∴OC=，
∴点B的坐标为（，0），点C的坐标为（，0），
∴；
（2）∵，∠AOC=90°，
∴
，
∵圆M与
轴正半轴相交于点
，即MA为半径，
∴AE是⊙M的切线；
（3）当△BP1G是直角三角形时，如图二所示，
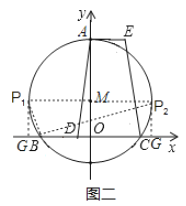
∵MA=MP1=4，点M的坐标为（0，2），
∴点P1的坐标为（-4，2）；
当△BP2G是直角三角形时，如图二所示，
∵MA=MP2=4，点M的坐标为（0，2），
∴点P2的坐标为（4，2）；
当△BP3G是直角三角形时，如图三所示，
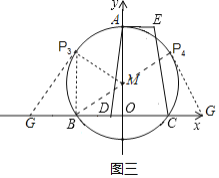
∵OB=，OM=2，
∴tan∠MBO=
，
∴∠MBO=30°，
∴∠MBP3=60°，
∵BM=MP3，
∴△BMP3是等边三角形，
∴BP3=4，
∴点P3的坐标为（，4）；
当△BP4G是直角三角形时，如图三所示，
∵BP4=8，∠P4BG=30°时，
∴点P4的纵坐标是：8×sin30°=8×
=4，
横坐标是：+8×cos30°=+8×
=，
∴点P4的坐标为（，4）；
由上可得，若△BPG为直角三角形，所有符合条件的点P的坐标是（-4，2），（4，2），（，4），（，4）．
