题目内容
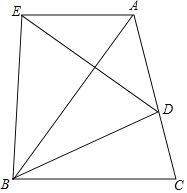
【题目】如图,已知△ABC是等边三角形,点D在AC边上一点,连接BD,以BD为边在AB的左侧作等边△DEB,连接AE,求证:AB平分∠EAC.
【答案】详见解析
【解析】
由等边三角形的性质得出AB=BC,BD=BE,∠BAC=∠BCA=∠ABC=∠DBE=60°,证出∠ABE=∠CBD,证明△ABE≌△CBD(SAS),得出∠BAE=∠BCD=60°,得出∠BAE=∠BAC,即可得出结论.
证明:∵△ABC,△DEB都是等边三角形,
∴AB=BC,BD=BE,∠BAC=∠BCA=∠ABC=∠DBE=60°,
∴∠ABC﹣∠ABD=∠DBE﹣∠ABD,
即∠ABE=∠CBD,
在△ABE和△CBD中,
∵AB=CB,
∠ABE=∠CBD,
BE=BD,,
∴△ABE≌△CBD(SAS),
∴∠BAE=∠BCD=60°,
∴∠BAE=∠BAC,
∴AB平分∠EAC.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
【题目】(数据收集)
以下是从某校九年级男生中随机选出的10名男生,分别测量了他们的身高(单位:cm),数据整理如下:
163 171 173 159 161 174 164 166 169 164
(数据分析)
确定这十个数据的众数、中位数、平均数,并填入表.
众数 | 中位数 | 平均数 |
|
|
|
(得出结论)
(1)若用样本中的统计量估计该校九年级男生平均身高,则这个统计量是 ;(选填“众数”或“中位数”或“平均数”中一个)
(2)若该校九年级共有男生280名,选用合适的统计量估计,该校九年级男生身高超过平均身高的人数.