题目内容
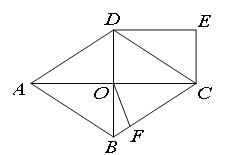
【题目】如图，在
中，点
为
边中点，动点
从点出发，沿着
的路径以每秒1个单位长度的速度运动到
点，在此过程中线段
的长度
随着运动时间
的函数关系如图2所示，则
的长为( )
A.
B.
C.
D.
【答案】C
【解析】
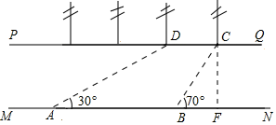
根据图象和图形的对应关系即可求出CD的长，从而求出AD和AC，然后根据图象和图形的对应关系和垂线段最短即可求出CP⊥AB时AP的长，然后证出△APC∽△ACB，列出比例式即可求出AB，最后用勾股定理即可求出BC．
解：∵动点
从点
出发，线段
的长度为
，运动时间为
的，根据图象可知，当=0时，y=2
∴CD=2
∵点为
边中点，
∴AD=CD=2，CA=2CD=4
由图象可知，当运动时间x=
时，y最小，即CP最小
根据垂线段最短
∴此时CP⊥AB，如下图所示，此时点P运动的路程DA＋AP=
所以此时AP=
∵∠A=∠A，∠APC=∠ACB=90°
∴△APC∽△ACB
∴
即
解得：AB=
在Rt△ABC中，BC=
故选C．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
【题目】参照学习函数的过程方法，探究函数
的图像与性质，因为
，即
，所以我们对比函数
来探究列表：
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … | |
| … |
|
| 1 | 2 | 4 | -4 | -2 | -1 |
|
| … | |
| … |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| … |
描点：在平面直角坐标系中以自变量
的取值为横坐标，以
相应的函数值为纵坐标，描出相应的点如图所示：
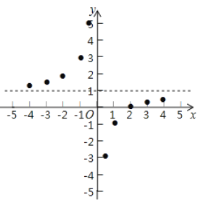
（1）请把
轴左边各点和右边各点分别用一条光滑曲线，顺次连接起来；
（2）观察图象并分析表格，回答下列问题：
①当
时，随的增大而______；（“增大”或“减小”）
②的图象是由
的图象向______平移______个单位而得到的；
③图象关于点______中心对称.（填点的坐标）
（3）函数与直线
交于点
，
，求
的面积.
