题目内容
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(﹣1,0)、B(4,0)、C(0,2)三点.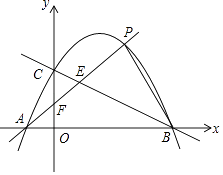
(1)求该二次函数的解析式;
(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;
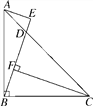
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2 , 求S1﹣S2的最大值.
【答案】
(1)
解:由题意可得 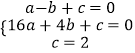 ,解得
,解得 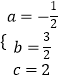 ,
,
∴抛物线解析式为y=﹣ ![]() x2+
x2+ ![]() x+2;
x+2;
(2)
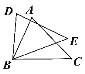
解:当点D在x轴上方时,过C作CD∥AB交抛物线于点D,如图1,
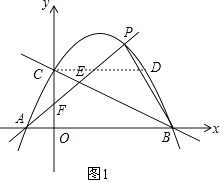
∵A、B关于对称轴对称,C、D关于对称轴对称,
∴四边形ABDC为等腰梯形,
∴∠CAO=∠DBA,即点D满足条件,
∴D(3,2);
当点D在x轴下方时,
∵∠DBA=∠CAO,
∴BD∥AC,
∵C(0,2),
∴可设直线AC解析式为y=kx+2,把A(﹣1,0)代入可求得k=2,
∴直线AC解析式为y=2x+2,
∴可设直线BD解析式为y=2x+m,把B(4,0)代入可求得m=﹣8,
∴直线BD解析式为y=2x﹣8,
联立直线BD和抛物线解析式可得 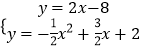 ,解得
,解得 ![]() 或
或 ![]() ,
,
∴D(﹣5,﹣18);
综上可知满足条件的点D的坐标为(3,2)或(﹣5,﹣18);
(3)
解:过点P作PH∥y轴交直线BC于点H,如图2,
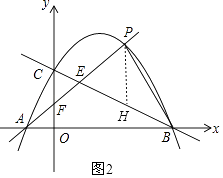
设P(t,﹣ ![]() t2+
t2+ ![]() t+2),
t+2),
由B、C两点的坐标可求得直线BC的解析式为y=﹣ ![]() x+2,
x+2,
∴H(t,﹣ ![]() t+2),
t+2),
∴PH=yP﹣yH=﹣ ![]() t2+
t2+ ![]() t+2﹣(﹣
t+2﹣(﹣ ![]() t+2)=﹣
t+2)=﹣ ![]() t2+2t,
t2+2t,
设直线AP的解析式为y=px+q,
∴ 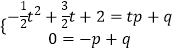 ,解得
,解得 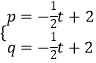 ,
,
∴直线AP的解析式为y=(﹣ ![]() t+2)(x+1),令x=0可得y=2﹣
t+2)(x+1),令x=0可得y=2﹣ ![]() t,
t,
∴F(0,2﹣ ![]() t),
t),
∴CF=2﹣(2﹣ ![]() t)=
t)= ![]() t,
t,
联立直线AP和直线BC解析式可得  ,解得x=
,解得x= ![]() ,即E点的横坐标为
,即E点的横坐标为 ![]() ,
,
∴S1= ![]() PH(xB﹣xE)=
PH(xB﹣xE)= ![]() (﹣
(﹣ ![]() t2+2t)(5﹣
t2+2t)(5﹣ ![]() ),S2=
),S2= ![]()
![]()
![]() ,
,
∴S1﹣S2= ![]() (﹣
(﹣ ![]() t2+2t)(5﹣
t2+2t)(5﹣ ![]() )﹣
)﹣ ![]()
![]()
![]() =﹣
=﹣ ![]() t2+5t=﹣
t2+5t=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
∴当t= ![]() 时,有S1﹣S2有最大值,最大值为
时,有S1﹣S2有最大值,最大值为 ![]() .
.
【解析】(1)由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;(2)当点D在x轴上方时,则可知当CD∥AB时,满足条件,由对称性可求得D点坐标;当点D在x轴下方时,可证得BD∥AC,利用AC的解析式可求得直线BD的解析式,再联立直线BD和抛物线的解析式可求得D点坐标;(3)过点P作PH∥y轴交直线BC于点H,可设出P点坐标,从而可表示出PH的长,可表示出△PEB的面积,进一步可表示出直线AP的解析式,可求得F点的坐标,联立直线BC和PA的解析式,可表示出E点横坐标,从而可表示出△CEF的面积,再利用二次函数的性质可求得S1﹣S2的最大值.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.