题目内容
【题目】问题提出
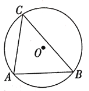
(1)如图,![]() 是
是![]() 的弦,点
的弦,点![]() 是
是![]() 上的一点,在直线
上的一点,在直线![]() 上方找一点
上方找一点![]() ,使得
,使得![]() ,画出
,画出![]() ,并说明理由;
,并说明理由;
问题探究
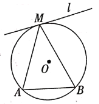
(2)如图,![]() 是
是![]() 的弦,直线
的弦,直线![]() 与
与![]() 相切于点
相切于点![]() ,点
,点![]() ,是直线
,是直线![]() 上异于点
上异于点![]() 的任意一点,请在图中画出图形,试判断
的任意一点,请在图中画出图形,试判断![]() 的大小关系;并说明理由;
的大小关系;并说明理由;
问题解决
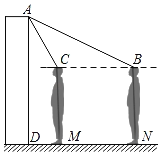
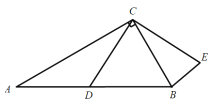
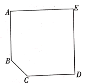
(3)如图,有一个平面图为五边形ABCDE的展览馆,其中![]() ,
,![]() ,
,![]() .展览馆保卫人员想在线段
.展览馆保卫人员想在线段![]() 上选一点
上选一点![]() 安装监控装置,用来监视边
安装监控装置,用来监视边![]() ,现只要使
,现只要使![]() 最大,就可以让监控装置的效果达到最佳,问在线段
最大,就可以让监控装置的效果达到最佳,问在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 最大?若存在,请求出符合条件的
最大?若存在,请求出符合条件的![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
【答案】(1)见解析 (2)∠AMB>∠AM1B,理由见解析; (3)存在;![]()
【解析】
(1)根据同弧所对的圆周角相等即可作图求解;
(2)根据三角形的外角定理即可作图求解;
(3)作经过点![]() 、
、![]() 且和
且和![]() 相切的
相切的![]() ,切点为
,切点为![]() ,由(2)可知此时
,由(2)可知此时![]() 最大,连接
最大,连接![]() 、
、![]() ,分别延长
,分别延长![]() 、
、![]() 交于点
交于点![]() ,证明四边形
,证明四边形![]() 是正方形,再求出
是正方形,再求出![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,由正方形的性质可得,
,由正方形的性质可得,![]() ,
,![]() ,再证明
,再证明![]() 垂直平分线段
垂直平分线段![]() ,再根据圆的性质可得
,再根据圆的性质可得![]() ,连接
,连接![]() ,可得
,可得![]() ,则
,则![]() ,设
,设![]() 的半径为
的半径为![]() ,则
,则![]() ,
,![]() ,在
,在![]() 中,利用勾股定理得到
中,利用勾股定理得到![]() 又利用
又利用![]() 得到OG=
得到OG= ![]() ,故可得到方程,求出R,再求出此时DM的长即可.
,故可得到方程,求出R,再求出此时DM的长即可.
解:(1)如图:
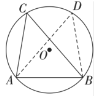
在优弧![]() 上任意取一点
上任意取一点![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() .
.
理由:![]() ,
,
∴![]() .
.
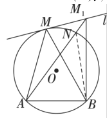
(2)![]() 如图,
如图,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
∵![]() 是
是![]() 的外角,
的外角,
∴![]() ,
,
∵![]()
∴![]()
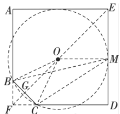
(3)作经过点![]() 、
、![]() 且和
且和![]() 相切的
相切的![]() ,切点为
,切点为![]() ,由(2)可知此时
,由(2)可知此时![]() 最大,
最大,
连接![]() 、
、![]() ,分别延长
,分别延长![]() 、
、![]() 交于点
交于点![]()
∵![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∵![]()
∴四边形![]() 是正方形。
是正方形。
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
连接![]() ,交
,交![]() 于点
于点![]() ,由正方形的性质可得,
,由正方形的性质可得,![]() ,
,
![]() ,
,
∵BF=CF,OB=OC
∴![]() 垂直平分线段
垂直平分线段![]() ,
,
∴圆心![]() 在线段
在线段![]() 上,
上,![]()
连接![]() ,则
,则![]() ,则
,则![]() ,
,
设![]() 的半径为
的半径为![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]()
∵![]()
∴![]() ,
,
∴![]() ,
,
解得![]() (不合题意,舍去)或
(不合题意,舍去)或![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴在线段![]() 上存在点
上存在点![]() ,使
,使![]() 最大,符合条件的
最大,符合条件的![]() 的长为
的长为![]() .
.

 名校课堂系列答案
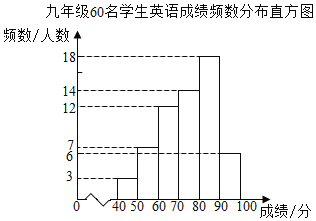
名校课堂系列答案【题目】在新冠病毒疫情防控期间,某校“停课不停学”,开展了网络教学.为了解九年级学生在网络学习期间英语学科和数学学科的学习情况,复课后从九年级学生中随机抽取60名学生进行了测试,获得了他们成绩(百分制)的数据,通过对成绩数据的整理、描述和分析,得到了如下部分信息.
①英语成绩的频数分布直方图如图:
(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100.)
②英语和数学成绩的平均数、中位数、众数如表:
学科 | 平均数 | 中位数 | 众数 |
英语 | 74.8 | m | 83 |
数学 | 72.2 | 70 | 81 |
③英语成绩在70≤x<80这一组的数据是:
70 71 72 73 73 73 74 76 77 77 77 78 79 79
根据以上信息,回答下列问题:
(1)表中m的值是 .
(2)在此次测试中,李丽的英语成绩为74分,数学成绩为71分,该名学生成绩排名更靠前的学科是 .(填“英语”或“数学”),理由是 .
(3)若该校九年级共有500名学生,请你估计英语成绩超过77.5分的人数.