ƒøƒ⁄»ð
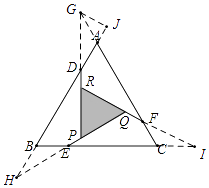
°æƒø°øŒ Â÷≥ˆ£∫»ÁÕº£®1£©£¨‘⁄±þ≥§Œ™a£®a£æ2£©µƒ’˝∑Ω–ŒABCD∏˜±þ…œ∑÷±Ωÿ»°AE=BF=CG=DH=1£¨µ±°œAFQ=°œBGM=°œCHN=°œDEP=45°„ ±£¨«ÛS’˝∑Ω–ŒMNPQ £Æ Œ ÂÃΩæø£∫∑÷±—”≥§QE£¨MF£¨NG£¨PH£¨ΩªFA£¨GB£¨HC£¨EDµƒ—”≥§œþ”⁄µ„R£¨S£¨T£¨W£¨ø…µ√°˜RQF£¨°˜SMG£¨°˜TNH£¨°˜WPE «Àƒ∏ˆ»´µ»µƒµ»—¸÷±Ω«»˝Ω«–Œ£®»ÁÕº£®2£©£©£Æ
£®1£©»ÙΩ´…œ ˆÀƒ∏ˆµ»—¸»˝Ω«–Œ∆¥≥…“ª∏ˆ–¬µƒ’˝∑Ω–Œ£®ŒÞ∑Ïœ∂£¨≤ª÷ÿµ˛£©£¨‘Ú–¬’˝∑Ω–Œµƒ±þ≥§Œ™£ª’‚∏ˆ–¬’˝∑Ω–Œ”Α≠’˝∑Ω–ŒABCDµƒ√ʪ˝”–∫Œπÿœµ£ª£®ÃÓ°∞£æ°±£¨°∞=°±°∞ªÚ£º°±£©£ªÕ®π˝…œ ˆµƒ∑÷Œˆ£¨ø…“‘∑¢œ÷S’˝∑Ω–ŒMNPQ”ÎS°˜FSB÷ƺ‰µƒπÿœµ «£∫
£®2£©Œ Ã‚Ω‚æˆ£∫«ÛS’˝∑Ω–ŒMNPQ £Æ
£®3£©Õÿ’𔶔√£∫»ÁÕº£®3£©£¨‘⁄µ»±þ°˜ABC∏˜±þ…œ∑÷±Ωÿ»°AD=BE=CF=1£¨‘Ÿ∑÷±π˝µ„D£¨E£¨F◊˜BC£¨AC£¨ABµƒ¥πœþ£¨µ√µΩµ»±þ°˜PQR£¨«ÛS°˜PQR £Æ £®«Î∑¬’’…œ ˆÃΩæøµƒ∑Ω∑®£¨‘⁄Õº3µƒª˘¥°…œ£¨œ»ª≠≥ˆÕº–Œ£¨‘ŸΩ‚戌 £©£Æ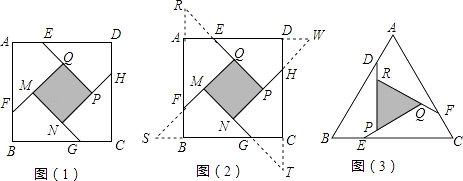
°æ¥∞∏°ø
£®1£©a£ª=£ªS’˝∑Ω–ŒMNPQ=4S°˜FSB
£®2£©Ω‚£∫°þS°˜FSB= ![]() °¡1°¡1=
°¡1°¡1= ![]() £¨
£¨
°ýS’˝∑Ω–ŒMNPQ=4S°˜FSB=4°¡ ![]() =2
=2
£®3£©Ω‚£∫»ÁÕºÀ˘ 棨°˜PDH£¨°˜QWEI£¨°˜RFG «»˝∏ˆ»´µ»µƒ»˝Ω«–Œ£¨ø…“‘∆¥≥…“ª∏ˆ∫Õ°˜ABC“ª—˘µƒµ»±þ»˝Ω«–Œ£®ŒÞ∑Ïœ∂£¨≤ª÷ÿµ˛£©£¨
°ýS°˜PRQ=S°˜ADG+S°˜BHE+S°˜CFI=3S°˜ADG£¨
»ÁÕº£¨π˝µ„G◊˜GJ°ÕBA”⁄J£¨
∏˘æð°œADG=°œBDP=30°„£¨°œDAF=60°„=°œGAJø…µ√£¨°œADG=°œAGD=30°„£¨
°ýAD=AG=1£¨
°ýGJ= ![]() AG=
AG= ![]() £¨
£¨
°ýS°˜ADG= ![]() AD°¡GJ=
AD°¡GJ= ![]() °¡1°¡
°¡1°¡ ![]() =
= ![]() £¨
£¨
°ýS°˜PQR=3S°˜ADG=3°¡ ![]() =
= ![]() £Æ
£Æ
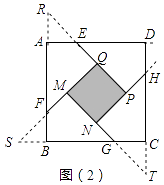
°æΩ‚Œˆ°øΩ‚£∫£®1£©Œ ÂÃΩæø£∫ °þAE=BF=CG=DH=1£¨°œAFO=°œBGM=°œCHN=°œDEP=45°„£¨
°ý°˜AER£¨°˜BFS£¨°˜CGT£¨°˜DHW «Àƒ∏ˆ»´µ»µƒµ»—¸÷±Ω«»˝Ω«–Œ£¨
°ýAE=DW£¨
°ýAE+DE=DW+DE=a£¨º¥AD=WE=a£¨
°þ∆¥≥…“ª∏ˆ–¬µƒ’˝∑Ω–ŒŒÞ∑Ïœ∂£¨≤ª÷ÿµ˛£¨
°ý’‚∏ˆ–¬’˝∑Ω–Œµƒ±þ≥§Œ™a£ª
°þÀ˘µ√µƒÀƒ∏ˆµ»—¸÷±Ω«»˝Ω«–Œµƒ–±±þ≥§Œ™a£¨‘Ú–±±þ…œµƒ∏þŒ™ ![]() a£¨
a£¨
√ø∏ˆµ»—¸÷±Ω«»˝Ω«–Œµƒ√ʪ˝Œ™£∫ ![]() a
a ![]() a=
a= ![]() a2 £¨
a2 £¨
°ý∆¥≥…µƒ–¬’˝∑Ω–Œ√ʪ˝Œ™£∫4°¡ ![]() a2=a2 £¨
a2=a2 £¨
º¥–¬’˝∑Ω–Œ”Α≠’˝∑Ω–ŒABCDµƒ√ʪ˝œýµ»£ª
°þ–¬’˝∑Ω–Œµƒ√ʪ˝=4°¡S°˜MSG=4°¡£®S°˜FSB+SÀƒ±þ–ŒMFBG£©£¨
‘≠’˝∑Ω–ŒABCDµƒ√ʪ˝=S’˝∑Ω–ŒMNPQ+4°¡SÀƒ±þ–ŒMFBG £¨
°ý4°¡£®S°˜FSB+SÀƒ±þ–ŒMFBG£©=S’˝∑Ω–ŒMNPQ+4°¡SÀƒ±þ–ŒMFBG £¨
º¥S’˝∑Ω–ŒMNPQ=4S°˜FSB£ª
À˘“‘¥∞∏ «£∫a£¨=£¨S’˝∑Ω–ŒMNPQ=4S°˜FSB£ª
°æøºµ„æ´Œˆ°ø∏˘æðƒøµƒ“—÷™Ãıº˛£¨¿˚”√µ»—¸÷±Ω«»˝Ω«–Œ∫Õµ»±þ»˝Ω«–Œµƒ–‘÷ µƒœýπÿ÷™ ∂ø…“‘µ√µΩŒ µƒ¥∞∏£¨–Ë“™’∆Œ’µ»—¸÷±Ω«»˝Ω«–Œ «¡ΩÃı÷±Ω«±þœýµ»µƒ÷±Ω«»˝Ω«–Œ£ªµ»—¸÷±Ω«»˝Ω«–Œµƒ¡Ω∏ˆµ◊Ω«œýµ»«“µ»”⁄45°„£ªµ»±þ»˝Ω«–Œµƒ»˝∏ˆΩ«∂ºœýµ»≤¢«“√ø∏ˆΩ«∂º «60°„£Æ

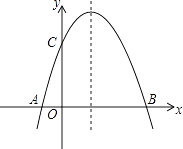
°æƒø°ø“—÷™∂˛¥Œ∫Ø ˝y=x2©Å2x
x | °≠ | ©Å1 | 0 | 1 | 2 | 3 | °≠ |
y | °≠ | 0 | ©Å1 | °≠ |
£®1£©«Î‘⁄±Ìƒ⁄µƒø’∏Ò÷–ÃӻΠµ±µƒ ˝£ª
£®2£©«Î‘⁄À˘∏¯µƒ∆Ω√Ê÷±Ω«◊¯±Íœµ÷–ª≠≥ˆy=x2©Å2xµƒÕºœÛ£ª
£®3£©µ±x‘Ÿ ≤√¥∑∂Œßƒ⁄ ±£¨yÀÊxµƒ‘ˆ¥Û∂¯ºı–°£ª
£®4£©π€≤Ïy=x2©Å2xµƒÕºœÛ£¨µ±x‘⁄ ≤√¥∑∂Œßƒ⁄ ±£¨y£æ0£Æ