题目内容
【题目】已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A,B两点(点A在点B的左侧,与y轴交于点C,点A、点B的横坐标是一元二次方程x2﹣4x﹣12=0的两个根.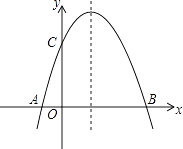
(1)请直接写出点A、点B的坐标.
(2)请求出该二次函数表达式及对称轴和顶点坐标.
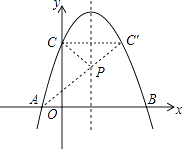
(3)如图,在二次函数对称轴上是否存在点P,使△APC的周长最小?若存在,请求出点P的坐标;若不存在,那个说明理由.
【答案】
(1)
解:解方程x2﹣4x﹣12=0得x1=﹣2,x2=6,
即A(﹣2,0),B(6,0)
(2)
解:将A、B两点坐标代入二次函数y=ax2+bx+6,
得到 ![]() ,
,
解得 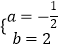 ,
,
即y=﹣ ![]() x2+2x+6,
x2+2x+6,
由于y=﹣ ![]() x2+2x+6=
x2+2x+6= ![]() (x﹣2)2+8,
(x﹣2)2+8,
即抛物线的对称轴为x=2,顶点坐标为(2,8)
(3)
解:如图,作点C关于抛物线对称轴的对称点C′,连接AC′,交抛物线对称轴于P点,连接CP,
∵C(0,6),
∴C′(4,6),
设直线AC′解析式为y=kx+n,
则 ![]() ,
,
解得 ![]() ,
,
∴y=x+2,
当x=2时,y=4,
即P(2,4).
【解析】(1)解一元二次方程x2﹣4x﹣12=0,求出点A和点B的横坐标,进而得到答案;(2)将A、B两点坐标代入二次函数y=ax2+bx+6,得到a和b的二元一次方程组,求出a和b的值即可,进而求出顶点坐标;(3)作点C关于抛物线对称轴的对称点C′,连接AC′,交抛物线对称轴于P点,连接CP,求出C′坐标,求出直线AC′解析式,进而求出点P的坐标.
【考点精析】掌握二次函数的概念和二次函数的图象是解答本题的根本,需要知道一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.

【题目】某商业集团新建一小车停车场,经测算,此停车场每天需固定支出的费用(设施维修费、车辆管理人员工资等)为800元.为制定合理的收费标准,该集团对一段时间每天小车停放辆次与每辆次小车的收费情况进行了调查,发现每辆次小车的停车费不超过5元时,每天来此处停放的小车为1440辆;当每辆次小车的停车费超过5元时,每增加1元,到此处停放的小车就减少120辆次.为便于结算,规定每辆次小车的停车费x(元)只取整数,用y(元)表示此停车场的日净收入,且要求日净收入不低于2512元.(日净收入=每天共收取的停车费一每天的固定支出)
A型利润 | B型利润 | |
甲店 | 200 | 170 |
乙店 | 160 | 150 |
(1)当x≤5时,写出y与x之间的关系式,并说明每辆小车的停车费最少不低于多少元;
(2)当x>5时,写出y与x之间的函数关系式(不必写出x的取值范围);
(3)该集团要求此停车场既要吸引客户,使每天小车停放的辆次较多,又要有较大的日净收入.按此要求,每辆次小车的停车费应定为多少元?此时日净收入是多少?