题目内容
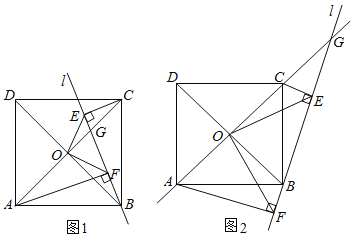
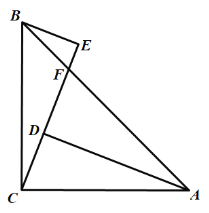
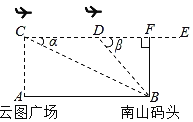
【题目】兴隆湖是成都天府新区著名的生态绿地工程.在一次户外综合实践活动中,小明同学所在的兴趣小组用无人机航拍测量云图广场A与南山码头B的直线距离.由于无人机控制距离有限,为了安全,不能直接测量,他们采用如下方法:如图,小明在云图广场A的正上方点C处测得南山码头B的俯角α=17.09°;接着无人机往南山码头B方向水平飞行0.9千米到达点D处,测得此时南山码头B的俯角β=45°.已知AC⊥AB,CD∥AB,请根据测量数据计算A,B两地的距离.(结果精确到0.1km,参考数据:sinα≈0.29,tanα≈0.31,sinβ≈0.71)
【答案】1.3千米
【解析】
根据题意设BF=x千米,由△BDF是等腰直角三角形得出DF=BF=x千米,在Rt△BCF中,根据tanα=![]() 列方程并求出x的值即可.
列方程并求出x的值即可.
解:设BF=x千米,
∵∠BFD=90°,∠β=45°,
∴DF=BF=x千米.
∵∠α=17.09°,
∴tanα=![]() =
=![]() =
=![]() ≈0.31,
≈0.31,
解得:x≈0.40,
∴AB=CF≈0.9+0.40≈1.3(千米).
答:A,B两地的距离约为1.3千米.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】成都市某公司自主设计了一款可控温杯,每个生产成本为16元,投放市场进行了试销.经过调查得到每月销售量y(万个)与销售单价x(元/个)之间关系是一次函数的关系,部分数据如下:
销售单价x(元/个) | … | 20 | 25 | 30 | 35 | … |
每月销售量y(万个) | … | 60 | 50 | 40 | 30 | … |
(1)求y与x之间的函数关系;
(2)该公司既要获得一定利润,又要符合相关部门规定(一件产品的利润率不得高于50%)请你帮助分析,公司销售单价定为多少时可获利最大?并求出最大利润.