题目内容
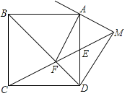
【题目】如图,梯形ABCD中,AD∥BC,DC⊥BC,且∠B=45°,AD=DC=1,点M为边BC上一动点,联结AM并延长交射线DC于点F,作∠FAE=45°交射线BC于点E、交边DCN于点N,联结EF.
(1)当CM:CB=1:4时,求CF的长.
(2)设CM=x,CE=y,求y关于x的函数关系式,并写出定义域.
(3)当△ABM∽△EFN时,求CM的长.
【答案】(1) CF=1;(2)y=![]() ,0≤x≤1;(3)CM=2﹣
,0≤x≤1;(3)CM=2﹣![]() .
.
【解析】
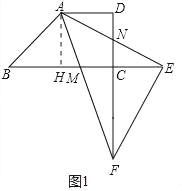
(1)如图1中,作AH⊥BC于H.首先证明四边形AHCD是正方形,求出BC、MC的长,利用平行线分线段成比例定理即可解决问题;
(2)在Rt△AEH中,AE2=AH2+EH2=12+(1+y)2,由△EAM∽△EBA,可得![]() ,推出AE2=EMEB,由此构建函数关系式即可解决问题;
,推出AE2=EMEB,由此构建函数关系式即可解决问题;
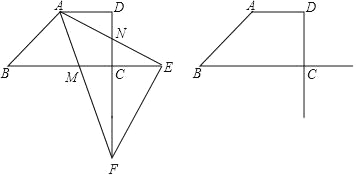
(3)如图2中,作AH⊥BC于H,连接MN,在HB上取一点G,使得HG=DN,连接AG.想办法证明CM=CN,MN=DN+HM即可解决问题;
解:(1)如图1中,作AH⊥BC于H.
∵CD⊥BC,AD∥BC,
∴∠BCD=∠D=∠AHC=90°,
∴四边形AHCD是矩形,
∵AD=DC=1,
∴四边形AHCD是正方形,
∴AH=CH=CD=1,
∵∠B=45°,
∴AH=BH=1,BC=2,
∵CM=![]() BC=
BC=![]() ,CM∥AD,
,CM∥AD,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴CF=1.
(2)如图1中,在Rt△AEH中,AE2=AH2+EH2=12+(1+y)2,
∵∠AEM=∠AEB,∠EAM=∠B,
∴△EAM∽△EBA,
∴![]() =
=![]() ,
,
∴AE2=EMEB,
∴1+(1+y)2=(x+y)(y+2),
∴y=![]() ,
,
∵2﹣2x≥0,
∴0≤x≤1.
(3)如图2中,作AH⊥BC于H,连接MN,在HB上取一点G,使得HG=DN,连接AG.
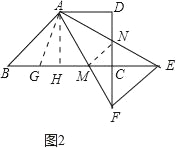
则△ADN≌△AHG,△MAN≌△MAG,
∴MN=MG=HM+GH=HM+DN,
∵△ABM∽△EFN,
∴∠EFN=∠B=45°,
∴CF=CE,
∵四边形AHCD是正方形,
∴CH=CD=AH=AD,EH=DF,∠AHE=∠D=90°,
∴△AHE≌△ADF,
∴∠AEH=∠AFD,
∵∠AEH=∠DAN,∠AFD=∠HAM,
∴∠HAM=∠DAN,
∴△ADN≌△AHM,
∴DN=HM,设DN=HM=x,则MN=2x,CN=CM=![]() x,
x,
∴x+![]() x=1,
x=1,
![]() ﹣1,
﹣1,
∴CM=2﹣![]() .
.