题目内容
【题目】如图,四边形ABCD是正方形,△ADF按顺时针方向旋转一定角度后得到△ABE,点E落在AD边上,若AF=4.AB=7.
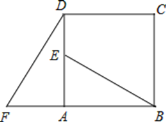
(1)旋转中心为 ;旋转角度为 ;
(2)求DE的长度;
(3)指出BE与DF的关系如何?并说明理由.
【答案】(1)旋转中心为点A,旋转角为∠BAD=90°;(2)3;(3)BE=DF,BE⊥DF,理由详见解析.
【解析】
(1)根据旋转的性质,点A为旋转中心,对应边AB、AD的夹角为旋转角;
(2)根据旋转的性质可得AE=AF,AD=AB,然后根据DE=ADAE计算即可得解;
(3)根据旋转可得△ABE和△ADF全等,根据全等三角形对应边相等可得BE=DF,全等三角形对应角相等可得∠ABE=∠ADF,然后求出∠ABE+∠F=90°,判断出BE⊥DF.
解:(1)旋转中心为点A,旋转角为∠BAD=90°;
(2)∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD﹣AE=7﹣4=3;
(3)BE、DF的关系为:BE=DF,BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°﹣90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE=DF,BE⊥DF.

【题目】某企业生产的一种果汁饮料由A、B两种水果配制而成,其比例与成本如下方表格所示,已知该饮料的成本价为8元/千克,按现价售出后可获利润50%,每个月可出售27500瓶.
每千克饮料所占比例 | 成本(元/千克) | |
A | 20% | m |
B | 80% | m-15 |
(1)求m的值;
(2)由于物价上涨,A水果成本提高了25%,B水果成本提高了20%,在不改变售价的情况下,若要保持每个月的利润不减少,则现在至少需要售出多少瓶饮料?