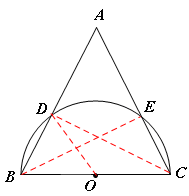
题目内容
如图,在△ABC中,以BC为直径作半圆0,交AB于点D,交AC于点E.AD=AE

(1)求证:AB=AC;
(2)若BD=4,BO= ,求AD的长.
,求AD的长.

(1)求证:AB=AC;
(2)若BD=4,BO=
 ,求AD的长.
,求AD的长.(1)见解析(2)6
解:(1)证明:连接CD、BE,
∵BC为半圆O的直径,∴∠BDC=∠CEB=900。
∴∠ADC=∠AEB=900。
又∵AD="AE" ,∠A=∠A,
∴△ADC≌△AEB(ASA)。∴AB=AC。
(2)连接OD,
∵OD=OB,∴∠OBD=∠ODB。
∵AB=AC,∴∠OBD=∠ACB。∴∠ODB=∠ACB
又∵∠OBD=∠ABC,∴△OBD∽△ABC。∴ 。
。
∵BO= ,∴BC=
,∴BC=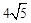 。
。
又∵BD=4,∴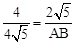 ,解得AB=10。
,解得AB=10。
∴AD=AB—BD=6。
(1)连接CD、BE,利用直径所对圆周角900,由ASA证明△ADC≌△AEB得AB="A" C。
(2)由△OBD∽△ABC得 ,求得AB=10,因此由 AD=AB—BD求解。
,求得AB=10,因此由 AD=AB—BD求解。
∵BC为半圆O的直径,∴∠BDC=∠CEB=900。
∴∠ADC=∠AEB=900。
又∵AD="AE" ,∠A=∠A,
∴△ADC≌△AEB(ASA)。∴AB=AC。
(2)连接OD,

∵OD=OB,∴∠OBD=∠ODB。
∵AB=AC,∴∠OBD=∠ACB。∴∠ODB=∠ACB
又∵∠OBD=∠ABC,∴△OBD∽△ABC。∴
 。
。∵BO=
 ,∴BC=
,∴BC=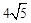 。
。又∵BD=4,∴
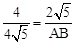 ,解得AB=10。
,解得AB=10。∴AD=AB—BD=6。
(1)连接CD、BE,利用直径所对圆周角900,由ASA证明△ADC≌△AEB得AB="A" C。
(2)由△OBD∽△ABC得
 ,求得AB=10,因此由 AD=AB—BD求解。
,求得AB=10,因此由 AD=AB—BD求解。
练习册系列答案
相关题目
 ,求由劣弧BC、线段CE和BE所围成的图形面积S.
,求由劣弧BC、线段CE和BE所围成的图形面积S.

 长为
长为 .
.
 的中点M.求证:AF=AB;
的中点M.求证:AF=AB;