题目内容
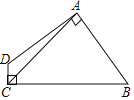
【题目】如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为( )
A. 15 B. 12.5 C. 14.5 D. 17
【答案】B
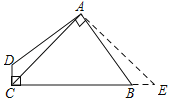
【解析】过A作AE⊥AC,交CB的延长线于E,判定△ACD≌△AEB,即可得到△ACE是等腰直角三角形,四边形ABCD的面积与△ACE的面积相等,根据S△ACE=![]() ×5×5=12.5,即可得出结论.
×5×5=12.5,即可得出结论.
如图,过A作AE⊥AC,交CB的延长线于E,
∵∠DAB=∠DCB=90°,
∴∠D+∠ABC=180°=∠ABE+∠ABC,
∴∠D=∠ABE,
又∵∠DAB=∠CAE=90°,
∴∠CAD=∠EAB,
又∵AD=AB,
∴△ACD≌△AEB,
∴AC=AE,即△ACE是等腰直角三角形,
∴四边形ABCD的面积与△ACE的面积相等,
∵S△ACE=![]() ×5×5=12.5,
×5×5=12.5,
∴四边形ABCD的面积为12.5,
故选B.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目