题目内容
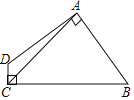
【题目】如图1,将长为10的线段OA绕点O旋转90°得到OB,点A的运动轨迹为![]() ,P是半径OB上一动点,Q是
,P是半径OB上一动点,Q是![]() 上的一动点,连接PQ.
上的一动点,连接PQ.
发现:∠POQ=________时,PQ有最大值,最大值为________;
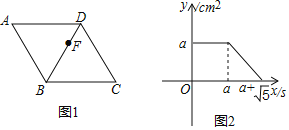
思考:(1)如图2,若P是OB中点,且QP⊥OB于点P,求![]() 的长;
的长;
(2)如图3,将扇形AOB沿折痕AP折叠,使点B的对应点B′恰好落在OA的延长线上,求阴影部分面积;
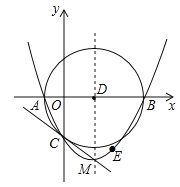
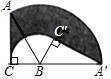
探究:如图4,将扇形OAB沿PQ折叠,使折叠后的弧QB′恰好与半径OA相切,切点为C,若OP=6,求点O到折痕PQ的距离.

【答案】发现: 90°,10![]() ; 思考:(1)
; 思考:(1)![]() ;(2)25π100
;(2)25π100![]() +100;(3)点O到折痕PQ的距离为
+100;(3)点O到折痕PQ的距离为![]() .
.
【解析】发现:先判断出当PQ取最大时,点Q与点A重合,点P与点B重合,即可得出结论;
思考:(1)先判断出∠POQ=60°,最后用弧长用弧长公式即可得出结论;
(2)先在Rt△B'OP中,OP2+(10![]() 10)2=(10-OP)2,解得OP=10
10)2=(10-OP)2,解得OP=10![]() 10,最后用面积的和差即可得出结论.
10,最后用面积的和差即可得出结论.
探究:先找点O关于PQ的对称点O′,连接OO′、O′B、O′C、O′P,证明四边形OCO′B是矩形,由勾股定理求O′B,从而求出OO′的长,则OM=![]() OO′=
OO′=![]() .
.
发现:∵P是半径OB上一动点,Q是![]() 上的一动点,
上的一动点,
∴当PQ取最大时,点Q与点A重合,点P与点B重合,
此时,∠POQ=90°,PQ=![]() =10
=10![]() ;
;
思考:(1)如图,连接OQ,
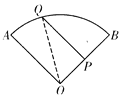
∵点P是OB的中点,
∴OP=![]() OB=
OB=![]() OQ.
OQ.
∵QP⊥OB,
∴∠OPQ=90°
在Rt△OPQ中,cos∠QOP=![]() ,
,
∴∠QOP=60°,
∴lBQ=![]()
(2)由折叠的性质可得,BP=B′P,AB′=AB=10![]() ,
,
在Rt△B'OP中,OP2+(10![]() 10)2=(10-OP)2
10)2=(10-OP)2
解得OP=10![]() 10,
10,
S阴影=S扇形AOB/span>-2S△AOP=![]()
=25π100![]() +100;
+100;
探究:如图2,找点O关于PQ的对称点O′,连接OO′、O′B、O′C、O′P,
则OM=O′M,OO′⊥PQ,O′P=OP=3,点O′是![]() 所在圆的圆心,
所在圆的圆心,
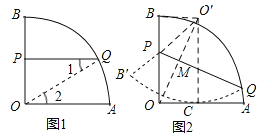
∴O′C=OB=10,
∵折叠后的弧QB′恰好与半径OA相切于C点,
∴O′C⊥AO,
∴O′C∥OB,
∴四边形OCO′B是矩形,
在Rt△O′BP中,O′B=![]() ,
,
在Rt△OBO′K,OO′=![]() ,
,
∴OM=![]() OO′=
OO′=![]() ×
×![]() =
=![]() ,
,
即O到折痕PQ的距离为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】在春季运动会上,某学校教工组和学生组进行定点投篮比赛,每组均派五名选手参加,每名选手投篮十次,投中记1分,不中记零分,3分以上(含3分)视为合格,比赛成绩绘制成条形统计图如下:
投篮成绩条形统计图
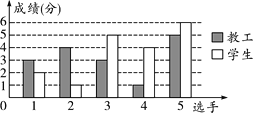
(1)请你根据条形统计图中的数据填写表格:
组别 | 平均数 | 中位数 | 方差 | 合格率 |
教工组 | ________ | 3 | ________ | 80% |
学生组 | 3.6 | ________ | 3.44 | 60% |
(2)如果小亮认为教工组的成绩优于学生组,你认为他的理由是什么?小明认为学生组成绩优于教工组,他的理由又是什么?
(3)若再让一名体育教师投篮后,六名教师成绩平均数大于学生组成绩的中位数,设这名体育教师命中m分,求m的值.