题目内容
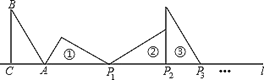
【题目】如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为S2,△B3C2B4的面积为S3,如此下去,则Sn=_____.

【答案】![]()
【解析】由AB1是边长为2的等边三角形ABC的高,利用三线合一得到B1为BC的中点,求出CB1的长,继而可得△B1CB2是有一个角为30度的直角三角形,同理可知△B2C1B3、△B3C2B4、△B4C3B5、…、都是有一个角为30度的直角三角形,而且后一个的斜边是前一个30度角所邻的直角边,由此即可求得Sn.
∵等边三角形ABC的边长为2,AB1⊥BC,
∴∠C=60°,CB1=BB1=1,
又∵∠B1B2C=90°,∴∠CB1B2=30°,
∴CB2=![]() ,B1B2=
,B1B2=![]() ,∴S1=
,∴S1=![]() ,
,
同理,Rt△B2C1B3中,B2C1=B1B2=![]() ,∴C1B3=
,∴C1B3=![]() ×
×![]() =
=![]() ,B2B3=
,B2B3=![]() ,
,
∴S2=![]() ,
,
同理,S3=![]()
…,
∴Sn=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】问题背景:
小红同学在学习过程中遇到这样一道计算题“计算![]() ”,他觉得太麻烦,估计应该有可以简化计算的方法,就去请教崔老师.崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
”,他觉得太麻烦,估计应该有可以简化计算的方法,就去请教崔老师.崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
获取新知:
请你和小红一起完成崔老师提供的问题:
(1)填写下表:
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
(2)观察表格,你发现![]() 与
与![]() 有什么数量关系?请直接写出
有什么数量关系?请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
解决问题:
(3)请结合上述的有关信息,计算![]() .
.