Question

如图，在梯形ABCD中，AD∥BC，AD=a，BC=b．
若E₁、F₁分别是AB、DC的中点，则E₁F₁=（AD+BC）=（a+b）；
若E₂，F₂分别是E₁B，F₁C的中点，则E₂F₂=（E₁F₁+BC）=[（a+b）+b]=（a+3b）；当E₃，F₃分别是E₂B，F₂C的中点，则E₃F₃=（E₂F₂+BC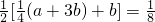）=（a+7b）；若E_nF_n分别是E_n-1，F_n-1的中点，根据上述规律猜想E_nF_n=________．（n≥1，n为整数）

Answer 1

分析：此题分别运用梯形的中位线定理，得到E₁F₁、E₂F₂的长；
根据求得的线段的长，发现规律：只有b的系数发生变化，且b的系数是2ⁿ-1．推而广之．
解答：根据题意，得在梯形ABCD中，AD∥BC，AD=a，BC=b．
若E₁、F₁分别是AB、DC的中点，则E₁F₁=（AD+BC）=（a+b）；
若E₂，F₂分别是E₁B，F₁C的中点，则E₂F₂=（E₁F₁+BC）=[（a+b）+b]=（a+3b）；
根据梯形中位线定理，推导可得E_nF_n=[a+（2ⁿ-1）b]=[a-b+2ⁿb]．
点评：本题是一道找规律的题目，这类题型在中考中经常出现．
对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．