题目内容
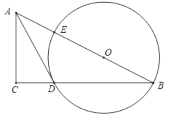
【题目】如图,在![]() 中,点
中,点![]() 在斜边
在斜边![]() 上,以
上,以![]() 为圆心,
为圆心,![]() 为半径作圆,分别与
为半径作圆,分别与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() ,连接
,连接![]() ,已知
,已知![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求劣弧
,求劣弧![]() 与弦
与弦![]() 所围阴影图形的面积;
所围阴影图形的面积;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连接![]() ,利用圆的半径相等及已知条件证明
,利用圆的半径相等及已知条件证明![]() ,再根据直角三角形两锐角互余得到
,再根据直角三角形两锐角互余得到![]() ,再根据平角定义即可得到结论;
,再根据平角定义即可得到结论;
(2)连接![]() ,作
,作![]() 于
于![]() ,根据
,根据![]() 及直角三角形的性质求出BD=2,根据垂径定理及三角函数求出,OF,再根据30
及直角三角形的性质求出BD=2,根据垂径定理及三角函数求出,OF,再根据30![]() 角所对的直角边等于斜边的一半求出OB,即可利用扇形面积减去三角形的面积求出阴影部分的面积;
角所对的直角边等于斜边的一半求出OB,即可利用扇形面积减去三角形的面积求出阴影部分的面积;
(3)先证明![]() 求出AB,再根据勾股定理求出半径,即可求得AE的长.
求出AB,再根据勾股定理求出半径,即可求得AE的长.
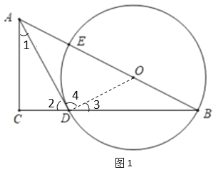
(1)证明:连接![]() ,如图1所示:
,如图1所示:
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
则![]() 为
为![]() 的切线;
的切线;
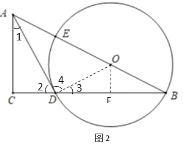
(2)连接![]() ,作
,作![]() 于
于![]() ,如图2所示:
,如图2所示:
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,
,
∴劣弧![]() 与弦
与弦![]() 所围阴影部分的面积
所围阴影部分的面积
![]() 扇形
扇形![]() 的面积
的面积![]() 的面积
的面积 ;
;
(3)∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ,或
,或![]() (舍去),
(舍去),
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴在![]() 中,
中, ![]() ,
,
∴设![]() 的半径为
的半径为![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目